Giá trị của biểu thức A = sin4x + cos4x - ¼cos 4x là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.

\(cos^3xsinx-sin^3xcosx=sinx.cosx\left(cos^2x-sin^2x\right)=\dfrac{1}{2}sin2x.cos2x=\dfrac{1}{4}sin4x\)
\(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2=1-\dfrac{1}{2}sin^22x\)
\(=1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{1}{4}\left(3+cos4x\right)\)

Chọn C.
Ta có: C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x)
= 2 [ (sin2x + cos2x) 2 - sin2x.cos2x]2 - [ (sin4x + cos4x)2 - 2sin4x.cos4x]
= 2[ 1 - sin2x.cos2x]2 - [ (sin2x+ cos2x) 2 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2[ 1- sin2x.cos2x]2 - [ 1 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2( 1 - 2sin2xcos2x+ sin4x.cos4x) –( 1- 4sin2xcos2x+ 4sin4xcos4x) + 2sin4x.cos4x
= 1.

1.Ý A
\(P=cos^4x-sin^4x=\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)=cos2x\)
2. Ý B
\(D=sin\left(\dfrac{5\pi}{2}-\alpha\right)+cos\left(13\pi+\alpha\right)-3sin\left(\alpha-5\pi\right)\)
\(=sin\left(2\pi+\dfrac{\pi}{2}-\alpha\right)+cos\left(\pi+\alpha+12\pi\right)-3sin\left(\alpha+\pi-6\pi\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+cos\left(\pi+\alpha\right)-3sin\left(\alpha+\pi\right)\)
\(=cos\alpha-cos\alpha+3sin\alpha=3sin\alpha\)
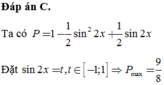
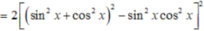

 không phụ thuộc vào x.
không phụ thuộc vào x.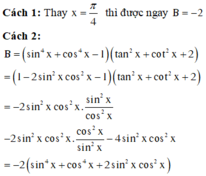
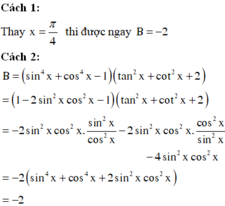
Chọn C.
Ta có A = sin4x + cos4x - ¼cos 4x = ( sin2x + cos2x) 2 - 2sin2x.cos2x - ¼cos 4x
= 1 - ½sin22x - ¼cos4x = 1 - ¼(1 – cos4x) - ¼cos4x = 3/4
giải thích giúp em đoạn biến đổi gần cuối đc ko ạ