Trong không gian Oxyz, viết phương trình mặt phẳng (P) chứa đường thẳng d 1 : x = 1 y = 1 - 2 t z = 1 + t và song song với đường thẳng d 2 : x - 1 1 = y 2 = z - 1 2 .
A. – 6 x - y + 2 z + 5 = 0
B. 6 x - y + 2 z - 7 = 0
C. 6 x + y - 2 z - 5 = 0
D. – 6 x + y + 2 z + 3 = 0



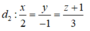

Chọn D.
Đường thẳng d1 đi qua điểm M1(1;1;1) vectơ chỉ phương u 1 → 0 ; - 2 ; 1
Đường thẳng d2 đi qua điểm M2(1;0;1) vectơ chỉ phương u 2 → 1 ; 2 ; 2
Gọi n → là một vectơ pháp tuyến của mặt phẳng (P), ta có:
Mặt phẳng (P) đi qua điểm M1(1;1;1) và nhận vectơ pháp tuyến có phương trình:
-6(x - 1) + 1(y - 1) + 2(z - 1) = 0 hay – 6x + y + 2z + 3 = 0.