Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng
d
1
,
d
2
lần lượt có phương trình
d
1
:
x
-
2
2
=
y
-
2
1
=
z
-
3
3
,
d
2
:
x
-
1
2
=
y
-
2
-
1
=
z
-
1
4
. Phương trình mặt phẳng (P)...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng d 1 , d 2 lần lượt có phương trình d 1 : x - 2 2 = y - 2 1 = z - 3 3 , d 2 : x - 1 2 = y - 2 - 1 = z - 1 4 . Phương trình mặt phẳng (P) cách đều hai đường thẳng d1;d2 là:
A. 7x – 2y - 4z = 0.
B. 7x – 2y - 4z + 3 = 0.
C. 2x+ y + 3z + 3 = 0
D. 14x – 4y – 8z + 3 = 0
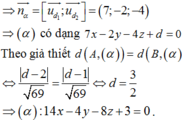
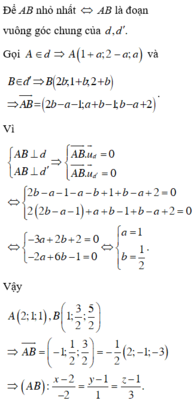
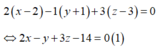
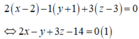
Chọn D.
Ta có d1 đi qua A(2;2;3) và có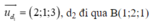
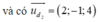
Do (P) cách đều d1;d2 nên (P) song song với d 1 , d 2
(P) có dạng 7x – 2y – 4z + d = 0
Vì (P) cách đều hai đường thẳng nên: d(A;(P)) = d(B;(P))