Giải phương trình : x4+(x +1)(5x2 - 6x - 6 ) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x4 + 5x2 + 1 = 0 (1)
Đặt x2 = t, t > 0.
(1) trở thành: t2 + 5t + 1 = 0 (2)
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 52 – 4.1.1 = 21 > 0
⇒ Phương trình có hai nghiệm:
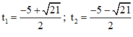
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

x4 – 5x2 + 4 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t2 – 5t + 4 = 0 (2)
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.

\(\Leftrightarrow\left(x^4+x^3-3x^2\right)-\left(x^3+x^2-3x\right)-\left(x^2+x-3\right)< 0\)
\(\Leftrightarrow x^2\left(x^2+x-3\right)-x\left(x^2+x-3\right)-1\left(x^2+x-3\right)< 0\)
\(\Leftrightarrow\left(x^2-x-1\right)\left(x^2+x-3\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1-\sqrt{13}}{2}< x< \dfrac{1-\sqrt{5}}{2}\\\dfrac{-1+\sqrt{13}}{2}< x< \dfrac{1+\sqrt{5}}{2}\end{matrix}\right.\)

Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm 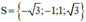
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
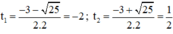
t 1 = - 2 < 0 nên loại.
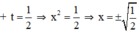
Vậy phương trình có tập nghiệm 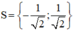
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
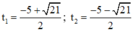
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

\(a,x^2-6x+5=0\\ \Rightarrow\left(x^2-5x\right)-\left(x-5\right)=0\\ \Rightarrow x\left(x-5\right)-\left(x-5\right)=0\\ \Rightarrow\left(x-1\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
\(b,2x^2+4x-8=0\\ \Rightarrow x^2+2x-4=0\\ \Rightarrow\left(x^2+2x+1\right)-5=0\\ \Rightarrow\left(x+1\right)^2-\sqrt{5^2}=0\\ \Rightarrow\left(x+1+\sqrt{5}\right)\left(x+1-\sqrt{5}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-1-\sqrt{5}\\x=-1+\sqrt{5}\end{matrix}\right.\)
\(c,4y^2-4y+1=0\\ \Rightarrow\left(2y-1\right)^2=0\\ \Rightarrow2y-1=0\\ \Rightarrow y=\dfrac{1}{2}\)
\(d,5x^2-x+2=0\)
Ta có:\(\Delta=\left(-1\right)^2-4.5.2=1-40=-39\)
Vì \(\Delta< 0\Rightarrow\) pt vô nghiệm

a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
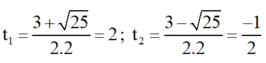
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
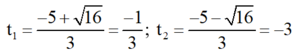
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

Phương trình bậc hai 5x2 – 6x + 1 = 0
Có: a = 5; b’ = -3; c = 1.; Δ’ = (b’)2 – ac = (-3)2 – 5.1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
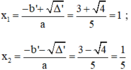

\(a,x^4-4x^3-19x^2+106x-120=0\\ \Rightarrow\left(x-4\right)\left(x^3-19x+30\right)=0\Rightarrow\left(x-4\right)\left(x+5\right)\left(x^2-5x+6\right)=0\\ \Rightarrow\left(x-4\right)\left(x+5\right)\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=-5\\x=2\\x=3\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-5;2;3;4\right\}\)
\(b,4x^4+12x^3+5x^2-6x-15=0\\ \Rightarrow\left(x-1\right)\left(4x^3+16x^2+21x+15\right)=0\\ \Rightarrow\left(x-1\right)\left[\left(4x^3+10x^2\right)+\left(6x^2+15x\right)+\left(6x+15\right)\right]=0\\ \Rightarrow\left(x-1\right)\left[2x^2\left(2x+5\right)+3x\left(2x+5\right)+3\left(2x+5\right)\right]=0\\ \Rightarrow\left(x-1\right)\left(2x+5\right)\left(2x^2+3x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{5}{2}\\2x^2+3x+3=0\left(vô.lí\right)\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{1;-\dfrac{5}{2}\right\}\)

BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn).
1) x2 - 11x + 38 = 0 ;
2) 6x2 + 71x + 175 = 0 ;
3) 5x2 - 6x + 27 =0 ;
4) - 30x2 + 30x - 7,5 = 0 ;
5) 4x2 - 16x + 17 = 0 ;
6) x2 + 4x - 12 = 0 ;

\(pt\Leftrightarrow x^4+5x^2\left(x+1\right)-6\left(x+1\right)^2=0\)
Đặt \(a=x^2;b=x+1\) ta có pt
\(a^2+5ab-6b^2=0\Leftrightarrow\left(a-b\right)\left(a+6b\right)=0\)
<=> a =b ; a = -6b
Giải từng trường hợp
Đấm vào chữ đúng giùm em ạ
Các đại ca đẹp zai,các cô nương xinh đẹp
Ai tick em là người như thế,100 người thôi.
Ming no mo ka djd