Cho hai đường thẳng a,b song song. Điểm A ∈ a , B ∈ b , C ∈ b . Biết B A a ^ = 40 o , A C B ^ = 30 o như hình vẽ. Câu nào sau đây đúng?
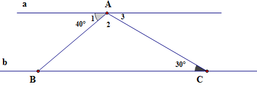
A. A 2 ^ > A 3 ^ > A B C ^
B. A 2 ^ > A B C ^ > A 3 ^
C. A B C ^ > A 2 ^ > A 3 ^
D. A 3 ^ > A B C ^ > A 2 ^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a d A c b
Ba đường thẳng a, b, c phân biệt mà a // b và b // c nên a // b.
Theo tiên đề Euclid, qua điểm A chỉ có một đường thẳng song song với đường thẳng b. Mà đó chính là đường thẳng a. Do đó nếu đường thẳng d khác đường thẳng a thì đường thẳng d không song song với đường thẳng b, tức là đường thẳng d cắt đường thẳng b. Tương tự, đường thẳng d cắt đường thẳng c.
Sửa lại chút bài làm của mình:
Ba đường thẳng a, b, c phân biệt mà a // c và b // c nên a // b.
Phần còn lại không cần sửa, mình nghĩ thế.

a) Vì a,b cùng vuông góc với đường thẳng AB nên a // b
b) Vì \(\widehat {{B_1}} = \widehat {{C_2}}( = 40^\circ )\). Mà 2 góc này ở vị trí so le trong nên b // c ( Dấu hiệu nhận biết 2 đường thẳng song song)
c) Vì a // b, b //c nên a // c

Bài giải
a b A B 1 3 2 4
a, Nếu \(\widehat{A_1}=120^o\text{ ; }\widehat{B_3}=130^o\text{ }\text{thì }a\text{ không song song }b\)
Muốn \(a\text{ }//\text{ }b\text{ thì }\orbr{\begin{cases}\widehat{A_1}=\widehat{B_3}=130^o\\\widehat{A_1}=\widehat{B_3}=120^o\end{cases}}\) để hai góc bằng nhau ( so le ngoài )
b, Nếu \(\widehat{A_2}=65^o\text{ ; }\widehat{B_3}=64^o\) thì a không song song b
Muốn \(a\text{ }//\text{ }b\text{ thì }\orbr{\begin{cases}\widehat{A}_2=\widehat{B_3}=65^o\\\widehat{A_2}=\widehat{B_3}=64^o\end{cases}}\) để hai góc bằng nhau

a)-d//b mà b cắt a nên d cắt a
-c//a mà a cắt b nên c cắt b
|
b) Các cặp đoạn thẳng sing song là:AB//CD ; AD//BC |