Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh độ dài AD, DC
A. AD > DC
B. AD < DC
C. AD = DC
D. Không so sánh được
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 8 2018
Kẻ DH ⊥ BC.
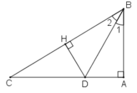
Xét hai tam giác vuông ABD và HBD, ta có:
∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).
Cạnh huyền BD chung
∠BAD = ∠BHD = 90º
Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)
⇒ AD = HD (2 cạnh tương ứng) (1)
Trong tam giác vuông DHC có ∠DHC = 90o
⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: AD < DC
JT
2 tháng 3 2018
Kẻ DE⊥ BC
Xét △ABC và △BDE có: Â=Ê=90*
∠ABD=∠DBE (BD phân giác ∠B)
BD: cạnh chung
⇒ △ABC = △BDE ( cạnh huyền-góc nhọn)
⇒ AD=DE ( 2 cạnh tương ứng)
Xét △EDC có: Ê=90*
⇒ Ê>∠C (theo nhận xét)
⇒ DC>DE (theo quan hệ góc,cạnh đối diện trong tam giác)
mà AD=DE ⇒DC>AD (đpcm)
22 tháng 2 2022
Câu B:
Xét hai tam giác vuông ABD và HBD, ta có:
∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).
Cạnh huyền BD chung
∠BAD = ∠BHD = 90º
Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)
⇒ AD = HD (2 cạnh tương ứng) (1)
Trong tam giác vuông DHC có ∠DHC = 90o
⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: AD < DC
13 tháng 3 2018
Xét hai tam giác vuông DBA và DHB có:
BD là cạnh chung
\(\widehat{ABD}=\widehat{DHB}\)( BD là tia phân giác )
\(\Rightarrow\Delta DBA=\Delta DBH\left(ch-gn\right)\)
\(\Rightarrow AB=DH\)( 2 cạnh bằng nhau )
Tam giác vuông DHC có:
DC là canh huyền suy ra DC là cạnh lớn nhất
\(\Rightarrow DC>DH\)
Mà DH = AD nên AD < DC
MD
18 tháng 2 2020
*Đảm bảo đúng 100% nhé!! 😊*
Giải:
Dựng DH vuông góc BC (H thuộc BC)
Xét hai tam giác vuông ABD và HBD có:
Góc A = Góc H (=90°)
BD: cạnh chung
Góc ABD = Góc HBD
=> Tam giác ABD = Tam giác HBD (cạnh huyền- góc nhọn)
=> AD = DH (2 cạnh tương ứng)
Xét tam giác vuông DHC vuông tại H có DC là cạnh huyền => DC là cạnh lớn nhất trong tam giác DHC
Do đó: AD = DH > DC (đpcm)
26 tháng 6 2022
Bài 2:
a: \(\widehat{ABD}=\dfrac{90^0-\widehat{C}}{2}\)
\(\widehat{ADB}=180^0-\widehat{BDC}=180^0-\left(\widehat{C}+\dfrac{\widehat{B}}{2}\right)=\dfrac{360^0-2\widehat{C}-\widehat{B}}{2}\)
\(\widehat{ADB}-\widehat{ABD}=\dfrac{\left(360^0-2\widehat{C}-\widehat{B}-90^0+\widehat{C}\right)}{2}\)
\(=\dfrac{270^0-\widehat{C}-\widehat{B}}{2}=\dfrac{270^0-90^0}{2}=90^0\)
=>\(\widehat{ADB}>\widehat{ABD}\)
=>AB>AD
b: Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
mà AB<BC
nên AD<CD
26 tháng 6 2022
Bài 2:
a: \(\widehat{ABD}=\dfrac{90^0-\widehat{C}}{2}\)
\(\widehat{ADB}=180^0-\widehat{BDC}=180^0-\left(\widehat{C}+\dfrac{\widehat{B}}{2}\right)=\dfrac{360^0-2\widehat{C}-\widehat{B}}{2}\)
\(\widehat{ADB}-\widehat{ABD}=\dfrac{\left(360^0-2\widehat{C}-\widehat{B}-90^0+\widehat{C}\right)}{2}\)
\(=\dfrac{270^0-\widehat{C}-\widehat{B}}{2}=\dfrac{270^0-90^0}{2}=90^0\)
=>\(\widehat{ADB}>\widehat{ABD}\)
=>AB>AD
b: Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
mà AB<BC
nên AD<CD
26 tháng 6 2022
a: Xét ΔBAD vuông tai A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
Do đó: ΔBAD=ΔBHD
Suy ra: AD=HD
b: ta có: AD=HD
mà HD<DC
nen AD<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tạiA có
BH=BA
góc HBK chung
Do đó:ΔBHK=ΔBAC
Suy ra BK=BC
hay ΔBKC cân tại B
CM
14 tháng 1 2019
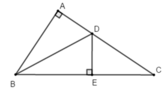
Từ D kẻ đường thẳng vuông góc với BC cắt BC tại E
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD cạnh huyền chung
A B D ^ = E B D ^ (BD là tia phân giác của góc B)
Khi đó: Δ A B D = Δ E B D (cạnh huyền góc nhọn)
Suy ra: AD = DE (hai cạnh tương ứng) (1)
Lại có tam giác DEC vuông tại E có DC là cạnh huyền
Suy ra DC > DE (trong tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất) (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC
Vậy A đúng, B, C, D sai.
Chọn đáp án A
Chọn B