Cho đường cong có phương trình là và điểm . Viết công thức chuyển hệ tọa độ trong phép tịnh tiến theo vectơ và viết phương trình của đường cong đối với hệ tọa độ . Từ đó suy ra là tâm đối xứng của .
Lần này , thì đừng có rảnh cho mấy học sinh lớp 1 đến ......
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 2 x + y = 5 m − 1 x − 2 y = 2
⇔ y = 5 m − 1 − 2 x x − 2 5 m − 1 − 2 x = 2 ⇔ y = 5 m − 1 − 2 x 5 x = 10 m
⇔ x = 2 m y = m − 1
Thay vào x 2 – 2 y 2 = − 2 ta có
x 2 – 2 y 2 = − 2 ⇔ ( 2 m 2 ) – 2 ( m − 1 ) 2 = − 2 ⇔ 2 m 2 + 4 m = 0 ⇔ m = 0 m = − 2
Vậy m ∈ {−2; 0}
Đáp án: C

Phương trình tiếp tuyến tại điểm M o ( x o ; y o ) là:
y – y o = y’( x o )(x – x o )
Trong đó:
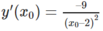
Ta có:
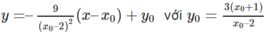
Để đường thẳng đó đi qua O(0; 0), điều kiện cần và đủ là:
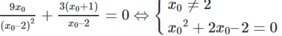
⇔ x o = –1 - 3 hoặc x o = –1 + 3
+) Với x o = –1 + 3 , ta có phương trình tiếp tuyến:
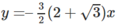
+) Với x o = –1 – 3 , ta có phương trình tiếp tuyến:
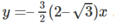

Ta có
3 x − y = 2 m + 1 x + 2 y = − m + 2 ⇔ 6 x − 2 y = 4 m + 2 x + 2 y = − m + 2 ⇔ 7 x = 3 m + 4 x + 2 y = − m + 2 ⇔ x = 3 m + 4 7 3 m + 4 7 + 2 y = − m + 2 ⇔ x = 3 m + 4 7 2 y = − 7 m + 14 7 − 3 m + 4 7 ⇔ x = 3 m + 4 7 y = − 5 m + 5 7
hệ phương trình có nghiệm duy nhất ( x ; y ) = 3 m + 4 7 ; − 5 m + 5 7
Để x – y = 1 thì 3 m + 4 7 − − 5 m + 5 7 = 1 ⇔ 8m – 1 = 7 ⇔ 8m = 8 m = 1
Vậy với m = 1 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x − y = 1
Đáp án: C


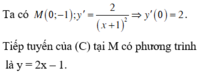
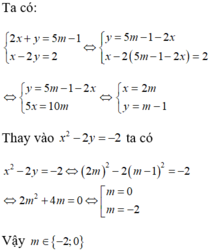




sao lại tự nhiên có "Unexpected text node:"
Khó ghê