OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học
Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025
Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho hình lập phương A B C D . A ' B ' C ' D ' . Gọi M, N lần lượt là trung điểm của AD, BB'. Cosin của góc hợp bởi MN và AC' bằng
A. 2 3
B. 3 3
C. 5 3
D. 2 4
Gọi cạnh của hình lập phương là a.
Suy ra
Cách 2. Gọi độ dài cạnh hình lập phương A B C D . A ' B ' C ' D ' là
Chọn hệ trục tọa độ Oxyz sao cho
Khi đó, tọa độ các đỉnh:
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B′C′ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B′D′ bằng
A. 5 a 5
B. a 3
C. 5 a
D. 3 a
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EF=AB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.
2. Cho tứ giác ABCD có AD=BC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEM=góc MFB.
3. Cho tam giác ABC (AB>AC). Trên cạnh AB lấy điểm D sao cho BD=AC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC = 2.BMN
4. Cho tứ giác ABCD, gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng các đường thẳng AA', BB', CC', DD' đồng quy.
5. Cho tam giác ABC, G là trọng tâm. Đường thẳng d không cắt các cạnh của tam giác ABC. Gọi A', B', C', G' lần lượt là hình chiếu của A, B, C, G trên đường thẳng d. Chứng minh GG'=AA'+BB'+CC'/3
Cho hình lập phương ABCD.A’B’C’D’. Gọi M,N,P lần lượt là trung điểm của các cạnh AB, AD, C’D’. Tính cosin góc giữa hai đường thẳng MN và CP
cho hình lập phương ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm A'B' và BC. chứng minh MN vuông góc AC'
help pls
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Gọi M,N lần lượt là trung điểm các cạnh A’B’ và A’D’(tham khảo hình vẽ). Cosin của góc tạo bởi hai mặt phẳng (CMN) và (AB’D’) bằng
A. 3 51 102
B. 51 102
C. 2 51 51
D. 51 51
Chọn đáp án D.
cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi O là tâm ABCD; M,N lần lượt là trung điểm AB,AD.
1. BD vuông góc (ACC'A') và A'C vuông góc(BDC'), A'C vuông góc AB', (BDC') vuông góc(ACC'A') và (MNC) vương góc (ACC'A')
2. Tính d(C,(BDC')),d(C,(MNC'))
3. Tính tan(AC,(MNC')) và tan((BDC'),(ABCD))
4. Tính cosin((MNC'),(BDC'))
5. Tính d(AB',BC')
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, A B = B C = a , A D = 2 a , S A vuông góc với mặt đáy A B C D , S A = a . Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa MN và (SAC).
A. 2 5
B. 55 10
C. 3 5 10
D. 1 5
Cho hình hộp đứng ABCD.A'B'C'D' có AB=AD=a, AA'=\(\frac{a\sqrt{3}}{2}\) ;\(\widehat{BAD}=60^o\) . Gọi M,N lần lượt là trung điểm của A'D' và A'B', E là giao điểm của MN và A'C'
a) Tính cosin của góc hợp bởi các cặp đường thằng:
BM và DN, BN và AC, BE và MC
b)Tính cosin của góc hợp bởi đường thẳng và mặt phẳng sau
BE và (ACC'A'), CE và (BB'D'B), BM và (ACN)
c) Chúng minh AC'vuông góc với mặt phẳng (BDMN)
d)Tính cosin của góc hợp bởi các cặp mặt phẳng:
(AMN) và (BDMN), (AB'D') và (EAD), (DA'C') và BMC)
Gọi cạnh của hình lập phương là a.
Suy ra
Cách 2. Gọi độ dài cạnh hình lập phương A B C D . A ' B ' C ' D ' là
Chọn hệ trục tọa độ Oxyz sao cho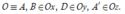
Khi đó, tọa độ các đỉnh: