Tìm các giá trị của m để phương trình 4 log a x 2 - log 1 2 x + m = 0 có nghiệm thuộc khoảng ( 0;1 )
A. m ≤ 1 4
B. m ≥ 1 4
C. 0 ≤ m ≤ 1 4
D. 0 < m < 1 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐK: x > 0
\(0< x< 1\Leftrightarrow\log_2x< 0\)
Đặt \(t=\log_2x\), pt đã cho trở thành \(t^2-2mt+m+2=0\) (1)
YCBT ↔ pt (1) có hai nghiệm âm phân biệt
\(\Leftrightarrow\begin{cases}\Delta'>0\\S< 0\\P>0\end{cases}\) \(\Leftrightarrow\begin{cases}m^2+3m+2>0\\2m< 0\\m+2>0\end{cases}\) \(\Leftrightarrow-1< m< 0\)

Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 

Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
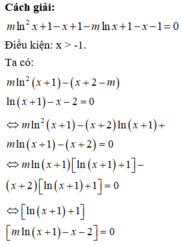
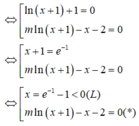

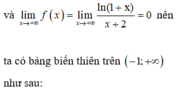
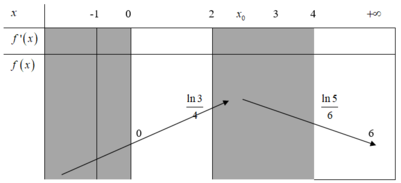

Phương trình đã cho tương ứng với log 2 2 x + log 2 x + m = 0 (*)
Đặt t = log 2 x ⇒ x = 2 t .Do 0 < x < 1 ⇒ 0 < 2 t < 1 ⇒ t < 0
Phương trình (*) thành t 2 + t + m = 0 ⇔ t 2 + t = - m (**)
Phương trình đã cho có nghiệm x ∈ 0 ; 1 ⇔ phương trình (**) có nghiệm t ∈ - ∞ ; 0
Xét hàm số f t = t 2 + t , t ∈ - ∞ ; 0
Ta có f ' t = 2 y + 1 ; f ' t = 0 ⇔ t = - 1 2
Lập bảng biến thiên và đi đến kết luận m ≤ 1 4
Đáp án A