Hình chóp tam giác đều có đường cao bằng h, các mặt bên hợp với đáy một góc 45 o . Tính diện tích đáy
A. S = h 2 3
B. S = 3 h 2 3
C. S = 3 3 4 h 2
D. S = 9 3 4 h 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.
Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.
Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.
Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).
Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI
Ta có
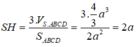
Ta lại có


Đáp án D
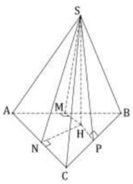
Theo giả thiết, các mặt bên tạo với đáy một góc 45 ° nên hình chiếu vuông góc của S trên (ABC) chính là tâm đường tròn nội tiếp ΔABC hay H là tâm đường tròn nội tiếp ΔABC .
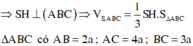
Áp dụng công thức Hê-rông em tính được p = 9 a 2 và S ΔABC = 3 15 a 2 4 .
Em lại có: S ΔABC = p . r với r là bán kính đường tròn nội tiếp tam giác ABC.
Từ H, em kẻ HM, HN, HP lần lượt vuông góc với AB, AC, BC thì
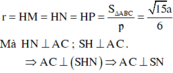
=> Góc giữa (SAC) và (ABC) chính là góc giữa SN và HN hay SNH ⏜ = 45 °


Do tam giác SAB đều và nằm trong mp vuông góc đáy \(\Rightarrow\) H là trung điểm AB
Gọi M là trung điểm AC\(\Rightarrow AM\perp AC\) (trung tuyến đồng thời là đường cao)
Gọi N là trung điểm AM \(\Rightarrow\) NH là đường trung bình tam giác AMH \(\Rightarrow NH||BM\Rightarrow NH\perp AC\)
\(\Rightarrow AC\perp\left(SNH\right)\)
Trong tam giác vuông SNH kẻ \(HK\perp SN\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(BM=\dfrac{a\sqrt{3}}{2}\Rightarrow NH=\dfrac{1}{2}BM=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}=\dfrac{20}{3a^2}\Rightarrow NH=\dfrac{a\sqrt{15}}{10}\)
Kẻ A M ⊥ B C và S H ⊥ A M , khi đó ∆ S H M vuông cân tại H. Suy ra H M = H S = h ; A M = 3 h
Vậy S = 9 3 4 h 2
Đáp án D