Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho S M S A = 2 3 . Một mặt phẳng (α) đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác có diện tích là:
A. 400 9 .
B. 16 9 .
C. 4 9 .
D. 20 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

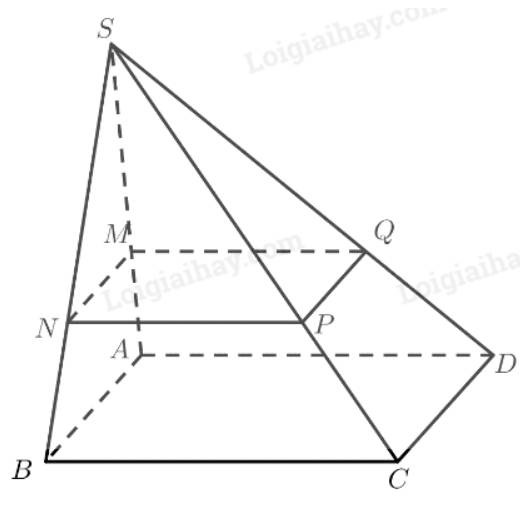
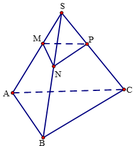
Qua \(M\) dựng đường thẳng song song với \(AB\), cắt \(SB\) tại \(N\).
Qua \(N\) dựng đường thẳng song song với \(BC\), cắt \(SC\) tại \(P\).
Qua \(M\) dựng đường thẳng song song với \(AD\), cắt \(SD\) tại \(Q\).
Ta có:
\(\left. \begin{array}{l}MN\parallel AB\\AB \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABCD} \right)\)
\(\left. \begin{array}{l}MQ\parallel AD\\AD \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABCD} \right)\)
\(\left. \begin{array}{l}MN\parallel \left( {ABCD} \right)\\MQ\parallel \left( {ABCD} \right)\\MN,MQ \subset \left( \alpha \right)\end{array} \right\} \Rightarrow \left( {MNPQ} \right)\parallel \left( {ABCD} \right)\)
\( \Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{{MN}}{{AB}}} \right)^2}\)
Ta có: \({S_{ABC{\rm{D}}}} = A{B^2} = {10^2} = 100\)
\(MN\parallel AB \Rightarrow \frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\)
\( \Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{2}{3}} \right)^2} = \frac{4}{9} \Rightarrow {S_{MNPQ}} = \frac{4}{9}{S_{ABC{\rm{D}}}} = \frac{4}{9}.100 = \frac{{400}}{9}\)
Chọn A.

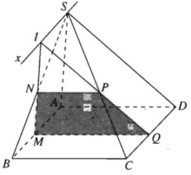
a) Vì M ∈ (SAB)
Và 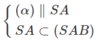 nên (α) ∩ (SAB) = MN
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và 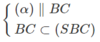 nên (α) ∩ (SBC) = NP
nên (α) ∩ (SBC) = NP
và NP // BC (1)
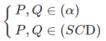 ⇒ (α) ∩ (SCD) = PQ
⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và 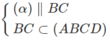 nên (α) ∩ (ABCD) = QM
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
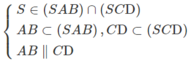 ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒ 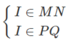
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.

Đáp án A
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2
Đáp án A
Qua M dựng đường thắng song song AB cắt SB tại N.
Qua M dựng đường thắng song song AD cắt SD tại Q.
Qua N dựng đường thắng song song BC cắt SC tại P.
Ta có M N // A B ⇒ M N // A B C D N P // B C ⇒ N P // A B C D .
⇒ M N P Q / / A B C D .
Tương tự câu 1 ta có tỉ lệ diện tích S M N P Q S A B C D = M N A B 2 = S M S A 2 = 4 9 .
Ta có S A B C D = 10.10 = 100 ⇔ S M N P Q = 100. 4 9 = 400 9