Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C.
y = (x + 1)(x – 2)2.
y' = 3x2 – 6x
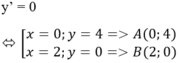
Khoảng cách giữa hai điểm cực trị AB = 2√5
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Đáp án C
Ta có
y ' = x 2 − 2 x − 1 ; y ' = 0 ⇔ x = 1 + 2 ⇒ y = − 8 − 4 2 3 x = 1 − 2 ⇒ y = − 8 + 4 2 3
Suy ra đồ thị hàm số đã cho có hai cực trị là A 1 + 2 ; − 8 − 4 2 3 và B 1 − 2 ; − 8 + 4 2 3 .
Vậy
A B = 1 − 2 − 1 + 2 2 + − 8 + 4 2 3 − − 8 − 4 2 3 2 = 10 2 3
Đáp án: D.
y' = 3 x 2 + 3x = 3x(x + 1) = 0
⇔ 
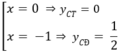
Vậy khoảng cách giữa hai điểm cực trị là:
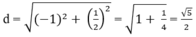
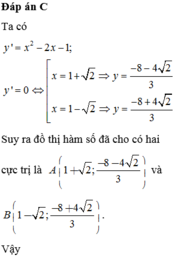
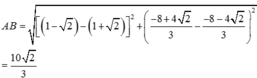
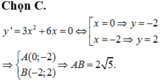
Đáp án A
Điều kiện: x ≠ − 1.
Ta có
y ' = 2 x − 1 x + 1 − x 2 + x x + 1 2 = 2 x 2 + x − 1 − x 2 + x x + 1 2 = x 2 + 2 x − 1 x + 1 2 = 0 ⇔ x = − 1 + 2 x = − 1 − 2 .
Hai điểm cực trị của đồ thị hàm số A − 1 + 2 ; 4 − 3 2 2 , B − 1 − 2 , − 4 − 3 2 2 .
Ta có A B = 2 2 2 + − 8 2 2 = 2 10 .