Lăng kính có chiết suất n = 2 và góc chiết quang A = 60 ° . Một chùm sáng đơn sắc hẹp được chiếu vào một bên AB của lăng kính với góc tới 30 ° . Tính góc ló của tia sáng khi ra khỏi lăng kính và góc lệch của tia ló và tia tới.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
24 tháng 8 2018
Áp dụng công thức lăng kính trong trường hợp góc chiết quang và góc tới nhỏ ta có góc lệch của tia ló và tia tới
VT
11 tháng 3 2019
Đáp án cần chọn là: B
Theo bài ra: i 1 = 45 0 , n = 2
sin i 1 = n sin r 1 ⇒ sin 45 0 = 2 sin r 1 ⇒ r 1 = 30 0 ⇒ r 2 = A – r 1 = 30 0
n sin r 2 = sin i 2 ⇒ 2 sin 30 0 = sin i 2 ⇒ i 2 = 45 0
Góc lệch: D = ( i 1 + i 2 ) – A = 30 0
VT
22 tháng 12 2019
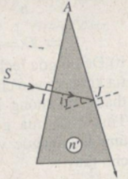
Ta có ở J trong trường hợp này (Hình 28.2G) :
n’sin i J = sin90 ° à n’ = 1/sin30 ° = 2
VT
28 tháng 9 2017
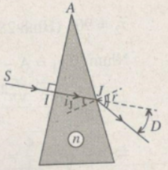
Ở I: i = 0 => r = 0.
Tia sáng truyền thẳng vào lăng kính (Hình 28.1G). Ở J : i J = 30 ° (góc có cạnh tương ứng vuông góc) :
sin r = n.sin i J = 3/2.1/2 = 0,75 => r = 48 ° 35'
Suy ra góc lệch :
D = r- i J = 48 ° 35' - 30 ° = 18 ° 35'
VT
18 tháng 8 2017
Đáp án cần chọn là: B
Ta có: D = n − 1 . A với góc chiết quang A nhỏ
Thay số: D = 1,5 − 1 .6 = 3 0
VT
28 tháng 12 2019
Do tính đối xứng nên:
r 1 = r 2 = A 2 = 30 ° i 1 = i 2 = A + D 2 = 60 + 30 2 = 45 °
Ta có: sin i 1 = n sin r 1 ⇒ n = sin i 1 sin r 1 = sin 45 0 sin 30 0 = 2 2. 1 2 = 2
VT
7 tháng 2 2017
Đáp án cần chọn là: B
Áp dụng định luật khúc xạ ánh sáng tại điểm tới I của mặt thứ nhất, ta có:
sin i 1 = n sinr 1 ↔ sin 45 = 2 sinr 1 → sinr 1 = 1 2 → r 1 = 30 0
Vì tia ló ra khỏi mặt thứ 2 đi vuông góc nên: i 2 = 0 → r 2 = 0
Ta có: A = r 1 + r 2 = 30 + 0 = 30 0
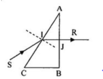
Áp dụng công thức lăng kính ta có: