Chứng minh rằng các bất đẳng thức
K
Khách
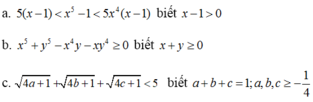
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 10 2019
2n + 1 > 2n + 3 (2)
+ Với n = 2 thì (2) ⇔ 8 > 7 (luôn đúng).
+ Giả sử (2) đúng khi n = k ≥ 2, nghĩa là 2k+1 > 2k + 3.
Ta chứng minh đúng với n= k+ 1 tức là chứng minh: 2k+2 > 2(k+ 1)+ 3
Thật vậy, ta có:
2k + 2 = 2.2k + 1
> 2.(2k + 3) = 4k + 6 = 2k + 2 + 2k + 4.
> 2k + 2 + 3 = 2.(k + 1) + 3 ( Vì 2k + 4 >3 với mọi k ≥ 2)
⇒ (2) đúng với n = k + 1.
Vậy 2n + 1 > 2n + 3 với mọi n ≥ 2.
LD
0
PV
3
MT
6 tháng 8 2015
ta có:
(a+b+c)3=a3+b3+c3+3a2b+3a2c+3b2a+3b2c+3c2a+3c2b+6abc
=a3+b3+c3+(3a2b+3a2c+3abc)+(3b2a+3b2c+3abc)+(3c2a+3c2b+3abc)-3abc
=a3+b3+c3+3a.(ab+ac+bc)+3b(ab+ac+bc)+3c.(ab+ac+bc)-3abc
=a3+b3+c3+3.(a+b+c)(ab+ac+bc)-3abc
=>03=a3+b3+c3+3.0.(ab+ac+bc)-3abc
0=a3+b3+c3-3abc
<=>a3 + b3 + c3 = 3abc
6 tháng 8 2015
a + b + c = 0 => a + b = -c
TA có
a^3 + b^3 + c^3 = ( a+ b)^3 - 3ab . ( a+ b) + c^3
Thay a +b = -c ta có
a^3 + b^3 + c^3 = -c^3 - 3ab.(-c) + c^3 = 3abc (ĐPCM)
CM
6 tháng 5 2018
a 3 b 3 = a 3 3 . b 3 3 = a b 3
Vế trái bằng vế phải nên đẳng thức được chứng minh.
PT
1
CM
17 tháng 9 2018
a b 2 3 = a b b 3 3 = 1 b a b 3 b ≠ 0
Vế trái bằng vế phải nên đẳng thức được chứng minh.
PT
1
CM
20 tháng 10 2017
Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.
PT
1
a) Ta có: x5 – 1 = (x – 1)(x4 + x3 + x2 + x + 1)
Lại có: x – 1 > 0 ⇒ x > 1 ⇒ x5 > x4 > x3 > x2 > x > 1
⇒ 1 + 1 + 1 + 1 + 1 < x4 + x3 + x2 + x + 1 < x4 + x4 + x4 + x4 + x4
hay 5 < x4 + x3 + x2 + x + 1 < 5x4
⇒ 5.(x – 1) < (x – 1)(x4 + x3 + x2 + x + 1) < 5x4.(x – 1)
hay 5.(x – 1) < x5 – 1 < 5x4.(x – 1) (đpcm)
b) x5 + y5 – x4y – xy4 = (x5 - x4y) - (xy4 - y5)
= x4.(x – y) – y4.(x – y)
= (x4 – y4).(x – y)
= (x2 + y2)(x2 – y2)(x – y)
= (x2 + y2).(x + y)(x – y)(x – y)
= (x2 + y2)(x + y)(x – y)2
Mà x2 + y2 ≥ 0; x + y ≥ 0; (x – y)2 ≥ 0
⇒ x5 + y5 – x4y – xy4 ≥ 0.
c) Ta có: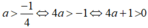
Tương tự. 4b +1 >0 và 4c +1 > 0
Áp dụng bất đẳng thức Cô-si cho hai số dương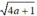
và 1 ta có:
Không có giá trị nào của a, b, c thỏa mãn hệ trên nên dấu “=” của BĐT không xảy ra.