Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dao động tổng hợp của vật đó là:
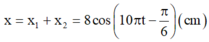
- Vận tốc của vật ở thời điểm là:
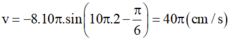
Chọn đáp án B.
Dao động tổng hợp của vật đó là:
x = x 1 = x 2 = 8 cos 10 π t − π 6 c m
Vận tốc của vật ở thời điểm t = 2s là:
v = − 8.10 π . sin 10 π .2 − π 6 = 40 π c m / s
Đáp án B
Dao động tổng hợp của vật đó là:
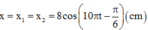
Vận tốc của vật ở thời điểm t = 2s là:
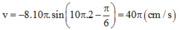
Đáp án B
Dao động tổng hợp của vật đó là
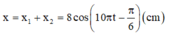
Vận tốc của vật ở thời điểm t=2(s) là:
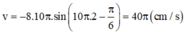
Đáp án B
Dao động tổng hợp của vật đó là: x = x 1 + x 2 = 8 cos 10 π t − π 6 c m
Vận tốc của vật ở thời điểm t = 2 s là:
v = − 8.10 π . sin 10 π .2 − π 6 = 40 π c m / s
Gọi phương trình dao động \(x=A\cos\left(\omega t+\varphi\right).\left(1\right)\)
Chu kỳ T là thời gian thực hiện 1 dao động toàn phần.
=> \(T=\frac{\Delta t}{N}=\frac{100}{50}=2s.\)
=> \(\omega=\frac{2\pi}{T}=\pi.\)(rad/s)
Áp dụng công thưc mối quan hệ giữa li độ tức thời x, biên độ A và vận tốc tại vị trí li độ đó v là
\(A^2=x^2+\frac{v^2}{\omega^2}=20^2+\frac{\left(4\pi\sqrt{3}\right)^2}{\pi^2}=448\Rightarrow A=21,166cm.\)
Mình nghĩ bài của bạn số hơi xấu?:))))
Li độ tại thời điểm \(\left(t+\frac{1}{3}\right)s\) là
Bạn có 2 cách để làm thay t ở công thức (1) bằng t+1/3s.
Tuy nhiên mình hay dùng cách 2 đường tròn như sau
Thời điểm t vật có li độ 20 cm thêm 1/3 s nữa thì góc quay được là \(\varphi=\frac{1}{3}.\pi.\)
Bài của bạn số xấu quá nên tìm góc cũng xấu.:))))))
\(\cos10^0=\frac{x}{A}\Rightarrow x=A\cos10^0\approx20,84cm.\)
Chọn đáp án B