Mắc một acquy 9V - r Ω vào nguồn điện AB có UAB = 12 V, dòng điện chạy từ A đến B. Công suất nạp điện của acquy là 27 W. Giá trị r là
A. 0,25 Ω
B. 0,5 Ω
C. 0,75 Ω
D. 1 Ω
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT
Vũ Thành Nam
6 tháng 2 2019
Đúng(0)
Những câu hỏi liên quan
VT
20 tháng 8 2017
Giả sử bộ nguồn này có m dãy, mỗi dãy gồm n nguồn mắc nối tiếp, do đó nm = 20. Suất điện động và điện trở trong của bộ nguồn này là :
E b = n E 0 = 2n;
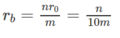
Áp dụng định luật Ôm cho toàn mạch ta tìm được cường độ dòng điện chạy qua điện trở R là :
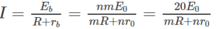
Để I cực đại thì mẫu số của vể phải của (1) phải cực tiểu. Áp dụng bất đẳng thức Cô-si thì mẫu số này cực tiểu khi : mR = n 0 . Thay các giá trị bằng số ta được : n = 20 và m = 1.
Vậy để cho dòng điện chạy qua điện trở R cực đại thì bộ nguồn gồm m = 1 dãy với n = 20 nguồn đã cho mắc nối tiếp.
VT
11 tháng 10 2017
Ta có: P = I 2 R = E R + r 2 R = 2 9 + 1 2 = 0 , 36 W H = U E .100 % = R R + r .100 % = 90 %
Chọn A
VT
14 tháng 6 2019
Thay các trị số đã cho và tìm được vào (1) ta tìm được giá trị cực đại của I là : I m a x = 10 A
VT
21 tháng 4 2018
đáp án B
ξ b = m ξ = 2 m r b = m r n = 0 , 1 m n = m 2 120 ⇒ I = ξ b R + r b = 2 m R + m 2 120 = 240 m + 120 m ≤ 120 R
⇒ I max = 120 R ⇔ m = 120 R = 6 ⇒ n = 2
29 tháng 11 2021
Dòng điện qua mạch:
\(I=\dfrac{\xi}{r+R}=\dfrac{12}{2+4}=2A\)
Công suất nguồn:
\(P=\xi\cdot I=12\cdot2=24W\)
Chọn C.