Hai điện tích q 1 < 0 và q 2 > 0 với | q 2 | > | q 1 | lần lượt đạt tại A và B như hình vẽ (I là trung điểm của AB). Điểm M có độ lớn điện trường tổng hợp do hai điện tích này gây ra bằng 0 nằm trên
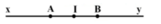
A. AI.
B. IB.
C. By
D. Ax.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

với EM = 0 áp dụng nguyên ký chồng chất điện trường: E1 +E2 =0 \(\Rightarrow\) \(\begin{cases}E_1=E_2\\\overrightarrow{E}_1\uparrow\downarrow\overrightarrow{E}_2\circledast\end{cases}\) TỪ\(\circledast\) và :\(\left|q_1\right|\) < \(\left|q_2\right|\) \(\Rightarrow\) M nằm trên AB và bên phía A
\(\Rightarrow\) -r1 +r2 =30 \(\otimes\)
lại có: E1 =E2 \(\Rightarrow\) k* \(\frac{\left|q_1\right|}{r^2_1}\)= k* \(\frac{\left|q_2\right|}{r^2_2}\)
\(\Leftrightarrow\)\(\frac{1}{r^2_1}\)= \(\frac{4}{r^2_2}\)\(\Rightarrow\)2 r1 -r2 = 0 \(\left(\otimes\otimes\right)\)
giải hệ pt \(\otimes\) và \(\left(\otimes\otimes\right)\) , ta được r1 =30; r2 =60
vậy M cách A 30cm
và cách B 60cm
![]()

1)lực tĩnh điện đẩy nhau cảu A và B là :
9*10^(9)*((1.8*10^(-8)*5.4*10^(-9))/0.03^(2))=9.72*10^(-4) N
gọi X là q c
vì tổng lục tĩnh điện tác dụng lên A ss with BC nên
ta có pt
9.72*10^(-4)+(9*10^(9)*((1.8*10^(-8)*X)/0.04^(2))=9*10^(9)*((5.4*10^(-9)*X)/0.056(2))
giải tìm được X=-1.8*10^(-8)
không chắc đúng đâu !
hình như sai cái gì đó chổ pt thay 0.05^(2) =>0.5^(2)
ta được X=-9.6*10^(-9)

Chọn đáp án D
Mặt phẳng (P) có vec-tơ pháp tuyến là n P ⇀ = 1 ; m ; - 1
Mặt phẳng (Q) có vec-tơ pháp tuyến là n Q ⇀ = m ; - 1 ; 1
Đường thẳng d m là giao tuyến của hai mặt phẳng (P) và (Q) nên có một vec- tơ chỉ phương là
![]()
Mặt phẳng (P) có vec-tơ pháp tuyến là n R ⇀ = 3 ; 1 ; 2
Để d m ⊥ R ⇔ Hai vec-tơ u ⇀ và n R ⇀ cùng phương
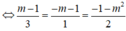
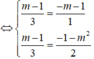
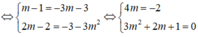
⇒ Không tồn tại giá trị m thỏa mãn yêu cầu bài toán.
Chọn D.
Các điện trường thành phần phải cùng phương ngược chiều và cùng độ lớn (điều này chỉ có thể trên khoảng Ax).