Cho đồ thị tọa độ - thời gian của một vật như hình sau:
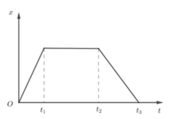
Vật chuyển động thẳng đều trong khoảng thời gian:
A. từ 0 đến t 2
B. từ t 1 đến t 2
C. từ 0 đến t 1 và từ t 2 đến t 3
D. từ 0 đến t 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Đồ thị tọa độ - thời gian của chuyển động thẳng đều là 1 đoạn thẳng. Đồ thị ứng đoạn từ t1 đến t2 cho thấy tọa độ x không thay đổi, tức vật đứng lại. Còn trong khoảng từ 0 đến t1 ta thấy quãng đường và thời gian tỉ lệ thuẩn với nhau nên trong khoảng thời gian này xe chuyển động thẳng đều.

Câu trả lời là: D. Không có lúc nào xe chuyển động thẳng đều.

a) Từ 0 đến \(\frac{T}{4}\): Wđ tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{4}\), Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{4}\).
Từ \(\frac{T}{4}\)đến \(\frac{T}{2}\): Wđ giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{2}\), Wt tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{2}\).
Từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\): Wđ tăng từ 0 đạt giá trị lớn nhất tại \(\frac{{3T}}{4}\),Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{{3T}}{4}\).
Từ \(\frac{{3T}}{4}\)đến T: Wđ giảm từ giá trị lớn nhất về 0 tại T, Wt tăng từ 0 đến giá trị lớn nhất tại T.
b) Tại thời điểm t = 0: Wđ = 0, Wt = W.
Tại thời điểm t = \(\frac{T}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
Tại thời điểm t = \(\frac{T}{4}\): Wđ = W, Wt = 0.
Tại thời điểm t = \(\frac{{3T}}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
→ ở mỗi thời điểm trên ta đều có: Wđ + Wt = W.

Chọn A.
Phương pháp: Tìm phương trình của vận tốc.
Cách giải: Đồ thị vận tốc trong khoảng thời gian 1 giờ đầu tiên có phương trình
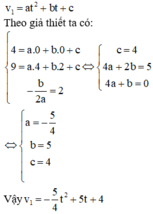
Quãng đường mà vật đã đi được trong 1 giờ đầu là

Vậy quãng đường mà vật di chuyển trong quãng thời gian
4 giờ đó là
![]()
Đáp án C