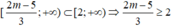Giá trị của m để bất phương trình 3x - 2m + 5 ≥ 0 có tập nghiệm là tập con của [2;+ ) là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2+2mx-2m+3>=0\)(1)
\(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(-2m+3\right)\)
\(=4m^2+8m-12\)
\(=4\left(m^2+2m-3\right)=4\left(m+3\right)\left(m-1\right)\)
Để bất phương trình (1) đúng với mọi x thuộc R thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4\left(m+3\right)\left(m-1\right)< =0\\1>0\end{matrix}\right.\)
=>\(\left(m+3\right)\left(m-1\right)< =0\)
TH1: \(\left\{{}\begin{matrix}m+3>0\\m-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-3\\m< 1\end{matrix}\right.\)
=>-3<m<1
TH2: \(\left\{{}\begin{matrix}m+3< 0\\m-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\)
=>\(m\in\varnothing\)

Chọn đáp án D.

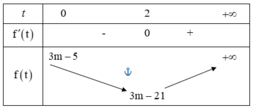
Từ bảng biến thiên trên, ta có bất phương trình đã cho có nghiệm khi và chỉ khi bất phương trình f(t) < 0
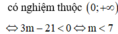


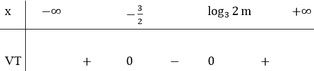
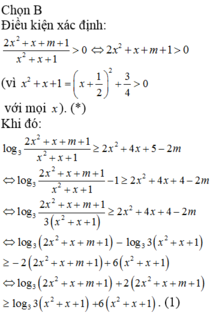

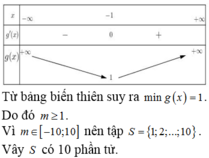




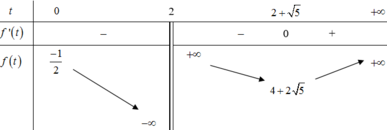

Chọn D.
Ta có:
Vậy tập nghiệm của bất phương trình là: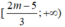
Để