Nếu thì bằng :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(sin\alpha=cos\beta=\dfrac{AB}{BC}\)
\(tan\alpha=cot\beta=\dfrac{AB}{AC}\)
\(\alpha+\beta=90^o\)
\(\Rightarrow\beta=90^o-\alpha\)
Theo đề bài :
\(sin\alpha=cos\beta\)
\(\Rightarrow sin\alpha=cos\left(90^o-\alpha\right)\)
mà \(\alpha;90^o-\alpha\) là 2 góc phụ nhau
\(\Rightarrow cos\left(90^o-\alpha\right)=sin\alpha\left(dpcm\right)\)
Tương tự \(tan\alpha=cot\beta=cot\left(90^o-\alpha\right)\)

a) Đúng.
(α) ⊥ (β) ⇒ ∃ đường thẳng d ⊂ (β) và d ⊥ (α ).
Mà (α ) // (γ)
⇒ d ⊥ (γ)
⇒ (β) ⊥ (γ).
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.
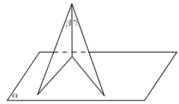

* Dựng \(\Delta OAB\)vuông tại A có: \(\widehat{AOB}=\alpha\)
Dựng \(\Delta OBC\)vuông tại B có: \(\widehat{BOC}=\beta\)và OC = 1 (đơn vị độ dài)
Từ C hạ \(CD\perp OA\)tại D \((D\in OA)\)
Từ B hạ \(BH\perp CD\)tại H (\(H\in CD\))
Ta có: \(\widehat{AOB}=\widehat{BCD}=\widehat{BCH}=\alpha\)(góc có cạnh tương ứng vuông góc)
Xét \(\Delta BOC\)có: \(\sin\beta=\frac{BC}{OC}=\frac{BC}{1}\Rightarrow BC=\sin\beta\)
\(\cos\beta=\frac{OB}{OC}=\frac{OB}{1}\Rightarrow OB=\cos\beta\)
Xét \(\Delta OAB\)có: \(\sin\alpha=\frac{AB}{OB}=\frac{AB}{\cos\beta}\Rightarrow AB=\sin\alpha.\cos\beta\)
Xét \(\Delta BCH\)có: \(\cos\alpha=\frac{CH}{BC}=\frac{CH}{\sin\beta}\Rightarrow CH=\cos\alpha.\sin\beta\)
Xét \(\Delta ODC\)có: \(\sin\left(\alpha+\beta\right)=\frac{DC}{OC}=\frac{DC}{1}=DC\)
Mà DC = DH + CH = AB + CH
=> \(\sin\left(\alpha+\beta\right)=\sin\alpha.\cos\beta+\cos\alpha.\sin\beta\)(1)
Cách dựng tương đối giống ở trên khác ở chỗ : OB =1 (đơn vị độ dài), \(\widehat{OCB}=90^o\), \(\widehat{BOC}=\beta,\widehat{AOB}=\alpha-\beta\),\(\widehat{AOC}=\alpha\)
Ta có: \(\widehat{BCH}=\widehat{BCD}=\widehat{AOC}=\alpha\)(góc có cạnh tương ứng vuông góc)
Xét \(\Delta BOC\)có: \(\sin\beta=\frac{BC}{OB}=\frac{BC}{1}=BC\Rightarrow BC=\sin\beta\)
\(\cos\beta=\frac{OC}{OB}=\frac{OC}{1}=OC\Rightarrow OC=\cos\beta\)
Xét \(\Delta OCD\)có:
\(\sin\alpha=\frac{CD}{OC}=\frac{CD}{\cos\beta}\Rightarrow CD=\sin\alpha.\cos\beta\)
Xét \(\Delta BCH\)có:
\(\cos\alpha=\frac{CH}{BC}=\frac{CH}{\sin\beta}\Rightarrow CH=\cos\alpha.\sin\beta\)
Xét \(\Delta OAB\)có:
\(\sin\left(\alpha-\beta\right)=\frac{AB}{OB}=\frac{AB}{1}=AB\)
Mà AB=DH= CD -CH = \(\sin\alpha.\cos\beta-\cos\alpha.\sin\beta\)
=> \(\sin\left(\alpha-\beta\right)=\sin\alpha.\cos\beta-\cos\alpha.\sin\beta\)(2)
Cộng từng vế của (1) và (2) ta được:
\(\sin\left(\alpha+\beta\right)+\sin\left(\alpha-\beta\right)=2.\sin\alpha.\cos\beta\)=> \(\sin\alpha.\cos\beta=\frac{\sin\left(\alpha+\beta\right)+\sin\left(\alpha-\beta\right)}{2}\)(đpcm)

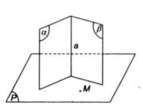

Vậy (MHK) chính là mặt phẳng đi qua M và vuông góc với (α) và (β).
Kết quả: Mặt phẳng (P) cần dựng (tức mp(MHK)) là mặt phẳng đi qua M và vuông góc với Δ.
Vì qua một điểm chỉ có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước nên (P) là duy nhất.
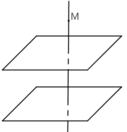
Nếu (α) // (β) thì qua M ta chỉ có thể vẽ một đường thẳng Δ vuông góc với (α) và (β). Bất kì mặt phẳng (P) nào chứa Δ cũng đều vuông góc với (α), (β). Trường hợp này, qua M có vô số mặt phẳng vuông góc với (α), (β).

α + β = 15 + (4 - 2i) = 19 - 2i ;
α – β = 15 - (4 - 2i) = 11 + 2i
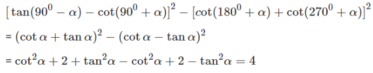
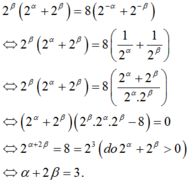
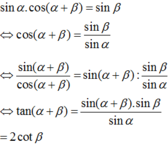
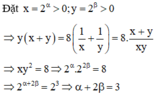
Chọn A.
Sử dụng công thức cộng ; ta có: