Cho tam giác ABC biết trực tâm H (1; 1) và phương trình cạnh AB: 5x- 2y+ 6=0, phương trình cạnh AC: 4x+ 7y -21= 0. Phương trình cạnh BC là:
A. 4x- 2y+1= 0
B. x- 2y + 14= 0
C.x- 2y+ 8 = 0
D. x- 2y- 14= 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

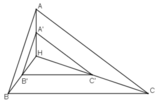
+ ΔABC nhọn ⇒ trực tâm H nằm trong ΔABC.
+ Gọi A’ = V(H; ½) (A)
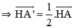
⇒ A’ là trung điểm AH.
+ Tương tự :
B’ = V(H; ½) (B) là trung điểm BH.
C’ = V(H; ½) (C) là trung điểm CH.
⇒ V(H; ½)(ΔABC) = ΔA’B’C’ với A’; B’; C’ là trung điểm AH; BH; CH.

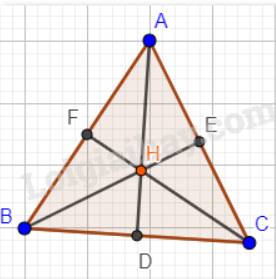
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.
Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD;
\(AD \bot BC; BE \bot AC; CF \bot AB\)
Xét tam giác ADB và tam giác ADC có:
AD chung
\(\widehat{ADB}=\widehat{ADC} (=90^0)\)
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).
Tương tự, ta cũng được, AC = BC
Xét tam giác ABC có AB = AC = BC nên là tam giác đều.
Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.

Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC, BH ⊥ AC, CH ⊥ AB
Trong ΔAHB, ta có:
AC ⊥ BH
BC ⊥ AH
Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
AB ⊥ CH
CB ⊥ AH
Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
BA ⊥ HC
CA ⊥ BH
Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.

Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)

Chọn D.
Gọi H (x; y) là trực tâm tam giác ABC nên
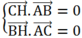
Mà
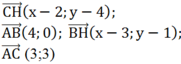
Suy ra:
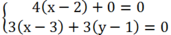
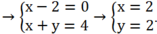
Vậy H(2; 2).
Đáp án :D
+Ta có hai đường thẳng AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ phương trình:
5 x - 2 y + 6 = 0 4 x + 7 y - 21 = 0 → A ( 0 ; 3 ) v à A H → ( 1 ; - 2 )
+Ta có BH vuông góc với AC nên đường thẳng BH qua H(1;1) và nhận vecto u → ( 4 ; 7 ) làm VTCP và u → ( 7 ; - 4 ) làm VTPT
Suy ra phương trình đường thẳng BH là:
7( x-1) – 4( y-1) =0
=> 7x- 4y -3= 0
+ ta có AB và BH cắt nhau tại B nên tọa độ điểm B là nghiệm hệ phương trình:
+Phương trình BC nhận A H → ( 1 ; - 2 ) là VTPT và qua B ( - 5 ; - 19 2 )
Suy ra phương trình (BC) :
Hay x-2y-14= 0 .