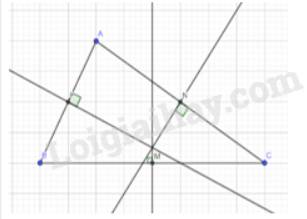
1.cho tam giác ABC nhọn M chuyển động trên BC vẽ trung trực của đoạn BM; CM cắt đường thẳng AB ;AC lần lượt tại E và F. Chứng Minh đường thẳng đi qua M vuông góc với EM đi qua một điểm cố định
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 12 2023
a: Sửa đề: Chứng minh ΔABD=ΔAMD
Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: DB=DM
=>D nằm trên đường trung trực của BM(1)
ta có: AB=AM
=>A nằm trên đường trung trực của BM(2)
Từ (1),(2) suy ra AD là đường trung trực của BM
23 tháng 12 2023
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
29 tháng 3 2023
a: Xet ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC
AM chung
=>ΔAMB=ΔAMC
b: I nằm trên trug trực của AB
nên IA=IB
=>ΔIAB cân tại I
24 tháng 6 2021
Do O thuộc đường trung trực của MC
\(\Rightarrow MO=OC\) (1)
Do O thuộc đường trung trực của BC
\(\Rightarrow OC=OB\) 2)
Từ (1) và (2) \(\Rightarrow OM=OB\)
Lại có: \(AM=AB\)
\(\Rightarrow AO\) là đường trung trực của BM
H
6 tháng 5 2022
Cậu tự vẽ hình
a. Xét tg ABC có:
BC2= 102=100
AB2 + AC2= 62 + 82 = 36 + 64 = 100
=> BC2=AB2 + AC2
=> Tam giác ABC vuông tại A (định lý Py-ta-go đảo)
b. Xét △BKM và △CKD vuông tại K có:
MK chung
BK=KC (K là trung điểm BC)
=> △BKM = △CKD (2cgv)
=> BM=CM (2 cạnh tương ứng)
Xét △DMC vuông tại D và △AMB vuông tại A có:
MB=CM (cmt)
góc BMC chung
=> △DMC = △AMB (ch-gn)
=> AB=DC (2 cạnh tương ứng)