Đường tròn x2+ y2 - 10x -11= 0 có bán kính bằng bao nhiêu? A.6 B.2 C. 4 D.
6
...
Đọc tiếp
Đường tròn x2+ y2 - 10x -11= 0 có bán kính bằng bao nhiêu?
A.6
B.2
C. 4
D. 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 12 2019
Đáp án: D
(C): x 2 + y 2 + 6x - 8y - 11 = 0 ⇔ (x + 3 ) 2 + (y - 4 ) 2 = 11 + 25
⇔ (x + 3 ) 2 + (y - 4 ) 2 = 36 ⇔ (x + 3 ) 2 + (y - 4 ) 2 = 6 2
Vậy đường tròn (C) có tâm I(-3;4) và bán kính R = 6
CM
4 tháng 6 2019
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính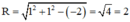 
b) 16x2 + 16y2 + 16x – 8y –11 = 0
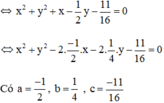
⇒ Đường tròn có tâm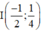 
, bán kính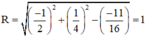 
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính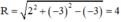 
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
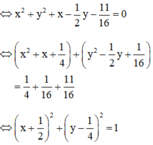
Vậy đường tròn có tâm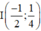 
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
PK
2
11 tháng 5 2022
\(\left(C\right):x^2-2x+1+y^2+8y+16-49=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y+4\right)^2=49=7^2\)
Vậy: Tâm là I(1;-4) và R=7
TP
1
13 tháng 7 2022
tâm là I(1,-4) bán kính là \(R=\sqrt{1+16-\left(-32\right)}=\sqrt{49}=7\)
CM
24 tháng 3 2017
Ta có: đường tròn (C1) :
Vậy (1) đúng
Đường tròn ( C2):
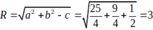
Vậy (2) đúng.
Chọn C.
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).
Ta có hệ số a= 5; b= 0 và c= -11 nên bán kính là R= a 2 + b 2 - c = 6
Chọn A.