Cho hàm số có đồ thị là . Tìm tất cả các giá trị của m để có ba điểm cực trị cùng với gốc tọa độ tạo thành bốn đỉnh của một hình thoi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

G/s (P),(d),(d1) cùng đi qua một điểm
Gọi I(a,b) là giao điểm của (P),(d),(d1)
Có \(I\in\left(P\right),\left(d\right),\left(d1\right)\)\(\Rightarrow\left\{{}\begin{matrix}b=a^2\left(1\right)\\b=a+2\left(2\right)\\b=-a+m\left(3\right)\end{matrix}\right.\)
Từ (1);(2)\(\Rightarrow a^2=a+2\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-1\end{matrix}\right.\)
TH1: Tại \(a=2\Rightarrow b=a^2=4\)
Thay \(a=2;b=4\) vào (3) ta được:\(4=-2+m\) \(\Leftrightarrow m=6\)
TH2: Tại \(a=-1\Rightarrow b=a^2=1\)
Thay \(a=-1;b=1\) vào (3) ta được:\(1=1+m\) \(\Leftrightarrow m=0\)
Vậy m=6 hoặc m=0
Phương trình hoành độ giao điểm của (d) và (P):
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)(*)
Ta có: \(a-b+c=1-\left(-1\right)+\left(-2\right)=0\)
Do đó phương trình (*) có 2 nghiệm phân biệt
\(x_1=-1;x_2=\dfrac{-c}{a}=2\)
\(x_1=-1\) thì \(y_1=x_1^2=\left(-1\right)^2=1\)
\(x_2=2\) thì \(y_2=x_2^2=2^2=4\)
Vậy (d) và (P) cắt nhau tại 2 điểm phân biệt \(A\left(-1;1\right);B\left(2;4\right)\)
Do đó các đồ thị của (P), (d) và \(\left(d_1\right)\)cùng đi qua 1 điểm
\(\Leftrightarrow\left[{}\begin{matrix}A\in\left(d_1\right)\\B\in\left(d_1\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}1=1+m\\4=-2+m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=6\end{matrix}\right.\)
Vậy khi m=0 hoặc m=6 thì các đồ thị của (P),(d) và cùng đi qua 1 điểm
-Chúc bạn học tốt-

Pt hoành độ giao điểm:
\(\sqrt{2x^2-2x-m}-x-1=0\)
\(\Leftrightarrow\sqrt{2x^2-2x-m}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\2x^2-2x-m=x^2+2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x-1=m\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb \(x\ge-1\)
Từ đồ thị hàm \(y=x^2-4x-1\) ta thấy \(-5< m\le4\)

a) Để đồ thị hàm số \(y=\left(m-2\right)x+2\) đồng biến trên R.
=> \(m-2>0.\)
<=> \(m>2.\)
b) Đồ thị hàm số \(y=\left(m-2\right)x+2\) song song với đường thẳng \(y=5x+1.\)
=> \(m-2=5.\)
<=> \(m=7.\)
Câu 2
a) Để hs đã cho đồng biến trên R thì:
\(m-2>0\\ < =>m>2\)
b) Đề đths đã cho song song với đường thẳng \(y=5x+1\) thì:
\(m-2=5\\ < =>m=7\)

Chọn A.
Ta có 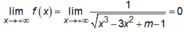
nên đồ thị hàm số có một đường tiệm cận ngang y = 0.
![]()
nên không tồn tại giới hạn
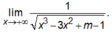
Do vậy đồ thị hàm số chỉ có một tiệm cận ngang y = 0.
Để đồ thị hàm số có bốn đường tiệm cận thì phương trình ![]() (1) có ba nghiệm phân biệt.
(1) có ba nghiệm phân biệt.
![]()
Số nghiệm của (2) là giao điểm của đường thẳng y = 1 –m và đồ thị hàm số ![]()
Xét hàm số ![]() Ta có
Ta có 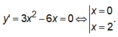
Bảng biến thiên
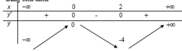
Dựa vào bảng biến thiên, ta thấy (2) có ba nghiệm phân biệt ⇔ -4 < 1-m < 0 ⇔ 1 < m < 5

a: Thay m=2 vào y=(m-1)x+m-1, ta được:
y=(2-1)x+2-1=x+1
Phương trình hoành độ giao điểm là:
x+1=-x+1
=>2x=0
=>x=0
Thay x=0 vào y=x+1, ta được:
y=0+1=1
Vậy: Tọa độ giao điểm là A(0;1)
b: Thay x=3 và y=4 vào y=(m-1)x+m-1, ta được;
3(m-1)+m-1=4
=>4(m-1)=4
=>m-1=1
=>m=2
c: Để hai đường thẳng này cắt nhau thì \(m-1\ne-1\)
=>\(m\ne0\)
Đáp án đúng : D