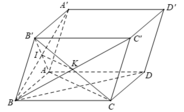
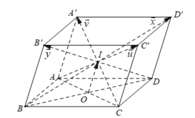
Cho hình hộp ABCD.EFGH . Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành BCGF. Trong các khẳng định sau, khẳng định nào đúng?
A. B D → , A K → , G F → đồng phẳng
B. B D → , I K → , G F → đồng phẳng
C. B D → , E K → , G F → đồng phẳng
D. B D → , I K → , G C → đồng phẳng

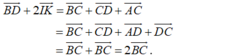
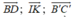 đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.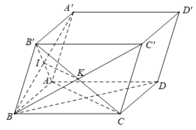
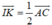
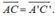
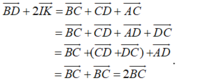
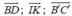 đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.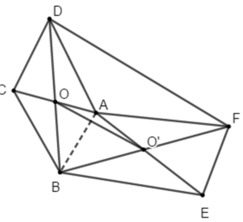
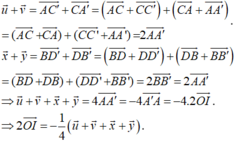

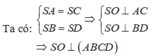
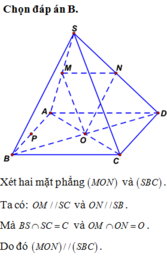
Chọn B.
- Ta có:
- + Các bộ véctơ ở phương án A, C, D không thể có giá cùng song song với một mặt phẳng.