Cho hai hình bình hành ABCD nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây là đúng? ...
Đọc tiếp
Cho hai hình bình hành ABCD nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
CM
20 tháng 9 2018
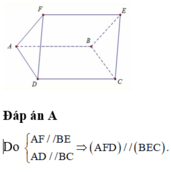
Phương án A sai vì AD và (BEF) cắt nhau tại A.
Phương án B đúng vì AD // BC, AF // BE
Phương án C sai vì (ABD) và (EFC) có điểm C chung
Đáp án B
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
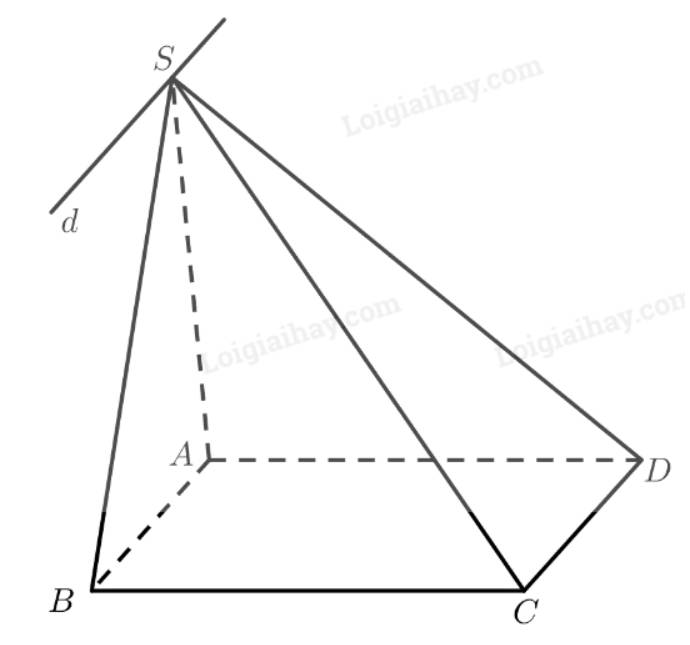
Ta có:
\(\left. \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\A{\rm{B}}\parallel C{\rm{D}}\\AB \subset \left( {SAB} \right)\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng \(d\) đi qua \(S\), song song với \(AB\) và \(C{\rm{D}}\).
Chọn A.
CM
25 tháng 11 2017
Đáp án C
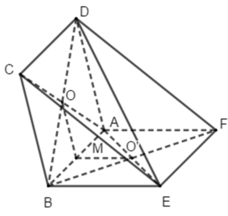
+) Ta có: BC // AD; BE // AF (ABCD và ABEF là hình bình hành)
Suy ra BC // (ADF); BE // (ADF)
Mà BC ∩ BE = B
Do đó (ADF) // (BEC).
+) O và O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O và O’ là trung điểm của BF và BD
Xét tam giác ABF có MO’ là đường trung bình nên MO’ // AF
MO’ // (ADF) (1)
Tương tự MO là đường trung bình của tam giác ABD nên MO // AD
MO // (ADF) (2)
Từ (1) và (2) suy ra (MOO’) // (ADF)
+) Chứng minh tương tự ta cũng có (MOO’) // (BCE).
+) Hai mặt phẳng (AEC) và (BDF) có:
AC ∩ DB = O ; AE ∩ BF = O’
Suy ra (AEC) ∩ (BDF) = OO’.
Vậy khẳng định (I); (II); (III) đúng.
CM
1 tháng 4 2017
Chọn A.
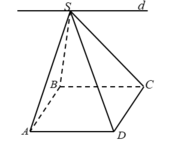
- Xét 2mp (SAD) và (SBC) có: Điểm S chung:
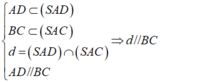
(Theo hệ quả của định lý 2 (Giao tuyến của ba mặt phẳng)).