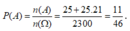Hai mươi lăm em học sinh lớp 12A được xếp ngồi vào một vòng tròn trong đêm lửa trại. Ba em học sinh được chọn ( xác suất được lựa chọn đối với mỗi em là như nhau ) và cử tham gia một trò chơi. Xác suất để ít nhất hai trong ba em học sinh được chọn ngồi cạnh nhau là
A
.
11
46
B
.
1
92
C
.
6
23
D
.
1
4
...
Đọc tiếp
Hai mươi lăm em học sinh lớp 12A được xếp ngồi vào một vòng tròn trong đêm lửa trại. Ba em học sinh được chọn ( xác suất được lựa chọn đối với mỗi em là như nhau ) và cử tham gia một trò chơi. Xác suất để ít nhất hai trong ba em học sinh được chọn ngồi cạnh nhau là
A . 11 46
B . 1 92
C . 6 23
D . 1 4
cách xếp thỏa mãn bài toán.
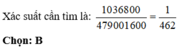
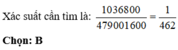
Chọn A
Gọi A là biến cố chọn được 3 em học sinh mà ít nhất 2 em trong đó ngồi cạnh nhau.
A 1 là biến cố chọn được 3 em học sinh ngồi cạnh nhau.
A 2 là biến cố chọn được 3 em học sinh mà trong đó chỉ có 2 em ngồi cạnh nhau.
Số phương án chọn ra 3 em từ 25 em là :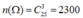
(cách).
Nhận thấy khi xét về 1 chiều, cứ 1 học sinh sẽ có duy nhất 1 học sinh khác ngồi cạnh. Việc đổi chiều sẽ tạo ra các phương án trùng lặp. Vậy để chọn ra 2 em ngồi cạnh nhau ta có: 25 (cách).
Số phương án để chọn ra 3 học sinh ngồi cạnh nhau cũng tương tự và có là: n A = 25 (cách).
Số phương án chọn học sinh thứ 3 sao cho học sinh này không ngồi cạnh 2 bạn kia là: 21(cách).
Số phương án chọn 3 học sinh sao cho có 2 em ngồi cạnh nhau là n A 2 = 25.21 = 525(cách).
Vậy xác suất xảy ra A là: