Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án : A
Giả sử mật khẩu là a1a2a3a4a5a6
Có 26 cách chọn a1
Có 9 cách chọn a2
Có 10 cách chọn a3
Có 10 cách chọn a4
Có 10 cách chọn a5
Có 10 cách chọn a6
Vậy theo qui tắc nhân ta có 26.9.10.10.10.10=2340000 mật khẩu.
Để gắn nhãn cho các ghế ta chọn chọn 1 chữ cái in hoa và 1 số (từ 1 đến 20).
Số cách chọn chữ cái in hoa: 26 cách (tương ứng với 26 chữ)
Số cách chọn số: 20 cách
Vậy số ghế gắn nhãn tối đa là 26.20 = 520 (ghế)
Đáp án C
Để tạo một biển số xe ta thực hiện các bước sau:
+ Chọn hai chữ cái cho phần đầu có 26 2 (mỗi chữ có 26 cách chọn)
+ Chọn 5 chữ số cho phần đuôi có 10 5 (mỗi chữ số có 10 cách chọn)
Vậy có thể tạo ra được 26 2 . 10 5 biển số xe
Đáp án C
Để tạo một biển số xe ta thực hiện các bước sau:
+ Chọn hai chữ cái cho phần đầu có 
(mỗi chữ có 26 cách chọn)
+ Chọn 5 chữ số cho phần đuôi có 
(mỗi chữ số có 10 cách chọn)
Vậy có thể tạo ra được 
biển số xe
Gọi số phần thưởng có thể được chia nhiều nhất là \(x\)(phần thưởng, \(x\inℕ^∗\))
Ta có:
\(374⋮x\\ 68⋮x\\ 340⋮x\)
\(x\) lớn nhất
\(\Rightarrow x=ƯCLN\left(374,68,340\right)\)
\(\Rightarrow\) Ta có:
\(374=2.187\\ 68=2^2.17\\ 340=2^2.5.17\)
⇒ BCNN(340,68,374) = 2.17 = 34
⇒ Vậy có thể chia được nhiều nhất 34 phần thưởng.
Mỗi phần thưởng có:
374 : 34 = 11(quyển vở)
68 : 34 = 2(cái thước)
340 : 34 = 10(nhãn vở)
Gọi số phần thưởng nhiều nhất có thể chia được là a ( a ∈ N* )
374 ⋮ a ; 68 ⋮ a ; 340 ⋮ a => a ∈ ƯC ( 374,68,340 )
Ta có :
374 = 2 . 11 . 17
68 = 22 . 17
340 = 22 . 5 . 17
=> ƯCLN(374,68,340) = 2 . 17 = 34
Mỗi phần thưởng có số quyển vở là :
374 : 34 = 11 ( quyển )
Mỗi phần thưởng có số cái thước là :
68 : 34 = 2 ( cái )
Mỗi phần thưởng có số nhãn vở là :
340 : 34 = 10 ( nhãn )
Vậy .....
Người ta muốn chia 374 quyển vở, 68 cái thước và 340 nhãn vở thành một số phần
thưởng như nhau nên số phần thưởng nhiều nhất thuộc ƯCLN( 374;68;340)
Ta có
374=2.11.17
68=2^2.17
340=2^2.5.17
=) UCLN (374; 68;340)=34
=) số phần thưởng nhiều nhất là 34
Chọn B
Gọi n là số nguyên dương nhỏ hơn 26.
Ta có : 0 < n < 26,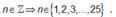
Chọn một chữ cái trong 24 chữ cái có 24 cách.
Chọn một số nguyên dương ( nhỏ hơn 26) có 25 cách.
Theo quy tắc nhân có : 24.25 = 600 cách ghi nhãn khác nhau.