Trong mp Oxy cho vecto v(1;2) và M(2;5). Tìm tọa độ ảnh M
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

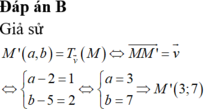

\(d'=T_{\overrightarrow{v}}\left(d\right)\)
Ta có: \(\left\{{}\begin{matrix}x'=x+a\\y'=y+b\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=x'-a=x'-3\\y=y'-b=y'-4\end{matrix}\right.\)
Thay vào pt \(\left(d\right):x+y-6=0\) ta đc:
\(\Rightarrow\left(x'-3\right)+\left(y'-4\right)-6=0\)
\(\Rightarrow x'+y'-13=0\)
Vậy \(\left(d'\right):x+y-13=0\)

gọi M có tọa độ là (x;y) do M thuộc Ox=> tọa ddoooj M là (x;0)
ta có : \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\left(-2-X;5\right)+\left(3-X;-1\right)+\left(7-X;1\right)\right|\)
=\(\left|\sqrt{\left(-2-X\right)^2+5^2}+\sqrt{\left(3-X\right)^2+1}+\sqrt{\left(7-X\right)^2+1}\right|\)
=> BẠN TÌ gtnn CÁI TRONG LÀ ĐC

Lời giải:
Phép tịnh tiến qua vecto $v$ biến $(d_3)$ thành chính nó thì $\overrightarrow{v}$ vecto chỉ phương của $(d_3)$
$\Rightarrow \overrightarrow{v}=(a,0)$
$T_{\overrightarrow{v}}(d_1)=d_2$
\(\Rightarrow \left\{\begin{matrix} 2x-y+2=0\\ 2(x+a)-y+1=0\end{matrix}\right.\Rightarrow a=\frac{1}{2}\)
Vậy $\overrightarrow{v}=(\frac{1}{2}, 0)$

Đáp án A
Vecto tịnh tiến cùng phương với d. Một vecto chỉ phương của d là u d → = ( 1 ; 2 )

Đáp án B
Vecto tịnh tiến cùng phương với d. Một vecto chỉ phương của d là u d → = 1 ; 2 .

Đáp án D
(d) biến thành chính nó khi vecto tịnh tiến cùng phương với (d). Mà (d) có một VTCP là 1 ; 2
