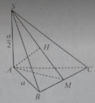
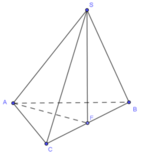
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
M là trung điểm của BC. Khi đó góc giữa hai mặt phẳng (SAM) và (SBC) bằng:
A. 0 o
B. 30 o
C. 45 o
D. 60 o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp
- Xác định góc giữa hai mặt phẳng (góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến).
Tính toán, sử dụng tính chất của tam giác vuông, tam giác đều
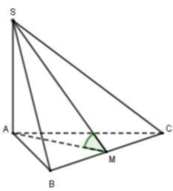


Phương pháp
- Xác định góc giữa hai mặt phẳng (góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến).
- Tính toán, sử dụng tính chất của tam giác vuông, tam giác đều.
Cách giải:
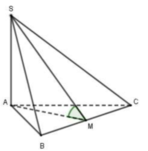
Gọi M là trung điểm của BC .
Tam giác ABC đều nên AM ⊥ BC . Mà
SA ⊥ (ABC) => SA ⊥ BC .
=> BC ⊥ (SAM) => BC ⊥ SM .
Ta có: 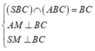
nên góc giữa hai mặt phẳng (SBC) và (ABC) là ![]()
Tam giác ABC đều cạnh a nên ![]()
Tam giác SAM vuông tại A nên ![]()
Chọn C.

Đáp án D
Góc giữa cạnh SA và đáy là S A F ^ ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
![]()
Vậy ![]()

Ta có : \(SA\perp BC\), \(AB\perp BC\) \(\Rightarrow SB\perp BC\)
Do đó : góc giữa 2 mặt phẳng (SBC) và (ABC) bằng \(\widehat{SBA}=30^0\)
\(V_{S.ABM}=\frac{1}{2}V_{S.ABC}=\frac{1}{2}SA.AB.BC\)
\(BC=AB=a;SA=AB.\tan30^0=\frac{a\sqrt{3}}{3}\)
Vậy \(V_{s.ABM}=\frac{a^3\sqrt{3}}{36}\)

a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ
tam giác ABC đều nên AM ⊥ BC ⇒ SM ⊥ BC (theo định lí ba đường vuông góc)
Đáp án B