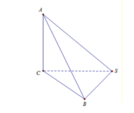
Hình chóp S.ABC có SB=SC=BC=CA=a Hai mặt phẳng (ABC) và (ASC) cùng vuông góc với (SBC) Thể tích khối chóp S.ABC bằng
![]()
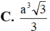
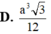
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Do hai mặt phẳng (ABC) và (ASC) cùng vuông góc với (SBC)
nên A C ⊥ S B C .
Lại có: S A B C = a 2 3 4 ; A C = a ⇒ V A . S B C = 1 3 A C . S S B C = a 3 3 12 .

Đáp án B
Phương pháp: Công thức tính thể tích khối chóp V = 1 3 S . h với S là diện tích đáy,h là chiều cao.
Chú ý tính chất hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng đó.
Cách giải: Ta có: A B C ⊥ S B C S B C ⊥ S B C A B C ∩ S A C = A C ⇒ A C ⊥ S B C
⇒ V = 1 3 S S B C . A C = 1 3 a a 2 3 4 = a 3 3 12

Chọn D.
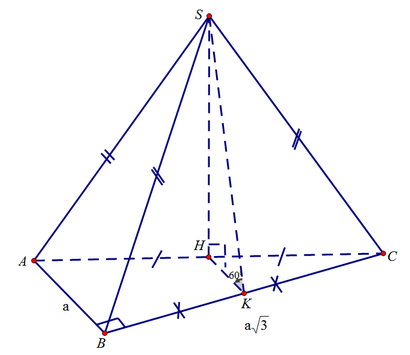
Từ giả thiết ta suy ra hình chiếu vuông góc H của S trên (ABC) trùng với tâm đường tròn ngoại tiếp Δ A B C .Mà Δ A B C vuông tại B nên H là trung điểm của AC. Kẻ HK//AB. Ta suy ra, K là trung điểm của BC và ta có góc giữa mặt bên (SBC) tạo với đáy là góc S K H ^ = 60 0 . Ta có H K = a 2 ⇒ S H = a 3 2 và S Δ A B C = a 2 3 2
Vậy V S . A B C = 1 3 S H . S Δ A B C = 1 3 a 3 2 . a 2 3 2 = a 3 4

Đáp án D
Gọi H là trung điểm của BC ta có: A H ⊥ B C Do A B C ⊥ S B C ⇒ A H ⊥ S B C
Đặt A H = x ⇒ H C = a 2 − x 2 = H B = S H ⇒ Δ S B C
vuông tại S (do đường trùng tuyến bằng cạnh đối diện). Suy ra B C = S B 2 + S C 2 = a 3 . Gọi O là tâm đường tròn ngoại tiếp Δ A B C ⇒ O ∈ A H ⇒ O A = O B = O C = OS .Ta có: R = R A B C = A C 2 sin B , trong đó sin B = A H A B = A S 2 − S H 2 A B = 1 2 Do đó R C = a ⇒ S x q = 4 π R 2 C = 4 π a 2 .