cho hàm số f (x) = 3 - x2. Tính f (-1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.

Đáp án B
Thay x = -1 vào hàm số ta được: f(x) = 3 - - 1 2 = 2 .

Đáp án B
Thay x = -1 vào hàm số ta được: f(x) = 3 - - 1 2 = 2 .

Chọn đáp án B
Phương pháp
Số điểm cực trị của hàm số y=f(x) là số nghiệm bội lẻ của phương trình f’(x)=0.
Cách giải
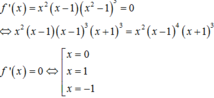
Tuy nhiên x=0 là nghiệm bội 2, x=1 là nghiệm bội 4 của phương trình f’(x)=0, do đó chúng không là cực trị của hàm số. Vậy hàm số có duy nhất 1 điểm cực trị x=-1.
Chú ý: HS nên phân tích đa thức f’(x) thành nhân tử triệt để trước khi xác định nghiệm, tránh sai lầm khi kết luận x=1 cũng là cực trị của hàm số.

Đáp án là D
Hàm số f(x) có đạo hàm là
![]()
f''(x) = 0 ![]()
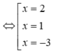
Bảng biến thiên

Từ BBT ta thấy hàm số có 2 điểm cực trị.
f′(x)=x3[f(x)]2⇔f′(x)[f(x)]2=x3f′(x)=x3[f(x)]2⇔f′(x)[f(x)]2=x3
Lấy nguyên hàm hai vế:
∫f′(x)[f(x)]2=∫x3⇔−1f(x)=x44+C∫f′(x)[f(x)]2=∫x3⇔−1f(x)=x44+C
f(2)=-1/5 <=> −1−15=244+C⇔C=1−1−15=244+C⇔C=1
Suy ra: −1f(x)=x44+1⇔f(x)=−4x4+4
vs fx= -1 ta có
\(f\left(-1\right)=3-\left(-1\right)2=3+2=5\)