Đồ thị hàm số y = x - 1 4 x + 7 có bao nhiêu điểm cực trị?
A. 3
B. 1
C. 2
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
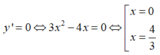
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.

b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Chọn D
+ Hàm phân thức hữu tỉ bậc nhất/ bậc nhất luôn đơn điệu trên các khoảng xác định của chúng,
do đó hàm này không có cực trị