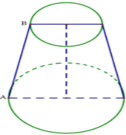
Có một cái cốc làm bằng giấy, được úp ngược như hình vẽ. Chiều cao của chiếc cốc là 20cm, bán kính đáy cốc là 4cm, bán kính miệng cốc là 5cm. Một con kiến đang đứng ở điểm A của miệng cốc dự định sẽ bò hai vòng quanh thân cốc để lên đến đáy cốc ở điểm B. Quãng đường ngắn nhất để con kiến có thể thực hiện được dự định của mình gần đúng nhất với kết quả nào dước đây?
![]()
![]()
![]()
![]()



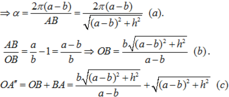

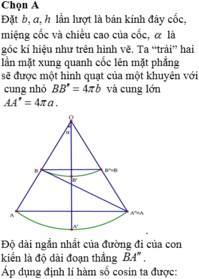
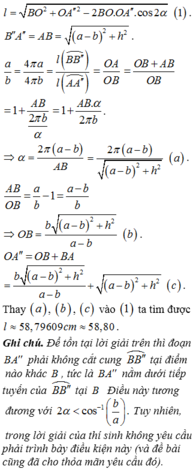






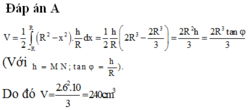
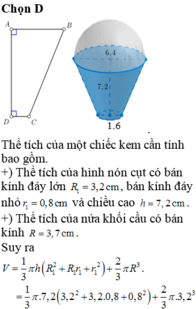

Đáp án đúng : A