Tính tích phân I = ∫ 0 1 x n 1 + x + x 2 2 ! + x 3 3 ! + . . . + x n n ! d x , n ∈ N * ta được kết quả
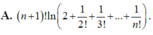
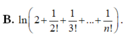
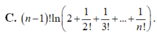
D. Đáp án khác.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(I=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\sqrt{3+2x-x^2}}=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\left(\sqrt{\left(x+1\right)\left(3-x\right)}\right)}\)
\(=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)^2\sqrt{\frac{3-x}{x+1}}}\)
Đặt \(t=\sqrt{\frac{3-x}{x+1}}\Rightarrow\frac{dx}{\left(x+1\right)^2}=-\frac{1}{2}\)
Đổi cận : \(x=-\frac{1}{2}\Rightarrow t=\sqrt{7};x=0\Rightarrow t=\sqrt{3}\)
\(I=-\frac{1}{2}\int\limits^{\sqrt{3}}_{\sqrt{7}}dt=\frac{1}{2}\left(\sqrt{7}-\sqrt{3}\right)\)

1) Ta có:
x³ + y³ + z³ - 3xyz = (x+y)³ - 3xy(x-y) + z³ - 3xyz
= [(x+y)³ + z³] - 3xy(x+y+z)
= (x+y+z)³ - 3z(x+y)(x+y+z) - 3xy(x-y-z)
= (x+y+z)[(x+y+z)² - 3z(x+y) - 3xy]
= (x+y+z)(x² + y² + z² + 2xy + 2xz + 2yz - 3xz - 3yz - 3xy)
= (x+y+z)(x² + y² + z² - xy - xz - yz).
Câu 2:
\(\frac{x^2-y^2+6x+9}{x+y+3}\)
\(=\frac{x^2-y^2+x^2+6x+9-x^2}{x+y+3}\)
\(=\frac{ \left(x+3\right)^2-y^2}{x+y+3}\)
\(=\frac{\left(x-y+3\right)\left(x+y+3\right)}{x+y+3}\)
\(=x-y+3\)

Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !
\(\left(x+6\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}\)
Vậy....
hk tốt
^^

Bài 1:
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^3-10x^2-6x\)
Bài 4:
a: =>3x+10-2x=0
=>x=-10
c: =>3x2-3x2+6x=36
=>6x=36
hay x=6
Bài 1:
\(a,=6x^3-10x^2+6x\\ b,=-2x^3-10x^2-6x\)
Bài 4:
\(a,\Leftrightarrow3x+10-2x=0\Leftrightarrow x=-10\\ b,\Leftrightarrow x\left(2x^2+9x-5\right)-\left(2x^3+9x^2+x+4,5\right)=3,5\\ \Leftrightarrow2x^3+9x^2-5x-2x^3-9x^2-x-4,5=3,5\\ \Leftrightarrow-6x=8\Leftrightarrow x=-\dfrac{4}{3}\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\)
Bài 1:
\(a,=7xy\left(2x-3y+4xy\right)\\ b,=x\left(x+y\right)-5\left(x+y\right)=\left(x-5\right)\left(x+y\right)\\ c,=\left(x-y\right)\left(10x+8\right)=2\left(5x+4\right)\left(x-y\right)\\ d,=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\\ =2x\left(4x+2\right)=4x\left(2x+1\right)\\ e,=5\left[\left(x-y\right)^2-4z^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x^2+8x-x-8=\left(x+8\right)\left(x-1\right)\\ g,\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\\ h,=x^2+3x+x+3=\left(x+3\right)\left(x+1\right)\)

\(\left(x-3\right)^2-5\left(x-2\right)+5=0\\ \Leftrightarrow x^2-6x+9-5x+10+5=0\\ \Leftrightarrow x^2-11x+24=0\\ \Leftrightarrow\left(x-8\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
\(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\\ \Leftrightarrow4x^2-4x+1-3\left(x^2-4\right)-25=0\\ \Leftrightarrow4x^2-4x-24-3x^2+12=0\\ \Leftrightarrow x^2-4x-12=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
a: Ta có: \(\left(x-3\right)^2-5\left(x-2\right)+5=0\)
\(\Leftrightarrow x^2-6x+9-5x+10+5=0\)
\(\Leftrightarrow x^2-11x+24=0\)
\(\Leftrightarrow\left(x-8\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
b: Ta có: \(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\)
\(\Leftrightarrow4x^2-4x+1-3x^2+12-25=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
Vì trong kết quả có xuất hiện ln, nên ta nghĩ đến ý tưởng dùng công thức
Đáp án: D