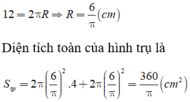Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Phương pháp: Tìm bán kinh đáy từ đó tính thể tích khối trụ.
Cách giải: Gọi r là bán kính đáy.
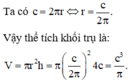
Gọi bán kính đáy là r.
Diện tích mặt đáy là:r x r x 3,14;chu vi mặt đáy là:r x 2 x 3,14.
Ta có: (r x r x 3,14):(r x 2 x 3,14)=3
r x r x 3,14 : r : 2 : 3,14=3
r x r : r x 3,14 : 3,14 : 2=3
r x 1 x 1 : 2=3
r : 2 = 3
r =3 x 2 = 6(cm)
Thể tích hình trụ là:(6x6x3,14)x6=678,24(cm3)
Đ/s:bán kính đáy:6 cm;thể tích hình trụ:678,24 cm3
Ta có : C = 13cm, h = 3cm
Diện tích xung quanh của hình trụ là :
S Xq = 2 π r ⋅ h = Ch = 13.3 = 39 cm 2
b) Ta có : r = 5mm, h = 8mm
Thể tích hình trụ là :
V = π r 2 h = π ⋅ 5 2 ⋅ 8 = 200 π ≈ 628 mm 3
Giải:
a) Ta có: C = 13m, h = 3cm
Diện tích xung quanh của hình trụ là: Sxp = 2 πr.h = C.h = 13.3 = 39 cm2
b) Ta có r = 5 mm , h = 8mm
Thể tích của hình trụ là:
V = πr2h = π.52.8 = 200π ≈ 628 mm3
Gọi đường chéo của hình thoi là d và chu vi đáy là p.
Ta có hệ phương trình sau:
d + d = 24cm (vì đường chéo của hình thoi bằng 24cm)
p = 52cm (vì chu vi đáy của hình thoi bằng 52cm)
Từ đó, ta có:
2d = 24cm
d = 12cm
Vậy đường chéo của hình thoi là 12cm.
Để tính chiều cao của hình lăng trụ, ta sử dụng định lý Pytago:
Chiều cao của hình lăng trụ = căn bậc hai của (d^2 - (cạnh đáy/2)^2)
= căn bậc hai của (12^2 - (10/2)^2)
= căn bậc hai của (144 - 25)
= căn bậc hai của 119
≈ 10.92cm
Vậy chiều cao của hình lăng trụ là khoảng 10.92cm.
Để tính thể tích của hình lăng trụ, ta sử dụng công thức:
Thể tích = diện tích đáy x chiều cao
= (diện tích hình thoi x 2) x chiều cao
= (cạnh đáy x cạnh đáy x sin(góc giữa hai đường chéo) x 2) x chiều cao
= (10cm x 10cm x sin(90°) x 2) x 10.92cm
= (100cm^2 x 1 x 2) x 10.92cm
= 2184cm^3
Vậy thể tích của hình lăng trụ là 2184cm^3
Đáp án C
Gọi R là bán kính của đường tròn
Theo giả thiết ta có:
