Cho parabol (P): y= x 2 + m . Gọi (d) là tiếp tuyến với (P) qua O có hệ số góc k>0. Xác định m để khi cho Oy quay quanh hình phẳng giới hạn bởi (P), (d) và trục Oy có thể tích bằng 6 π .
A. m = 4
B. m = 5
C. m = 6
D. m = 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Ta có
y = 2 x − x 2 ⇔ x − 1 2 = 1 − y ⇔ x = 1 + 1 − y x = 1 − 1 − y
với y ≤ 1 .
Thể tích khối tròn xoay cần tính là:
V y = π ∫ 0 1 1 − 1 − y 2 − 1 − 1 − y 2 d y
= 4 π ∫ 0 1 1 − y d t = 4 π . 2 3 = 8 π 3


Chọn D
D quay xung quanh trục Oy
Ta có: y = ( x - 2 ) 2 ⇔ x - 2 = ± y ⇔ x = 2 ± y
V = π ∫ 0 4 2 + y 2 - 2 - y 2 dy = 8 π . ∫ 0 4 y dy = 8 π . 2 3 y 3 2 | 0 π = 128 π 3 đ v t t

Đáp án D
Phương pháp:
Công thức tính thể tích hình phẳng được giới hạn bởi các đường thẳng x = a , x = b ( a < b ) và các đồ thị hàm số ư
y = f(x), y = g(x) khi quay quanh trục Ox là: V = π ∫ a b f 2 x - g 2 x dx
Cách giải:
Ta có công thức tính thể tích hình phẳng đã cho là:
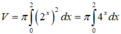

Đáp án B
y = 2 x + 1 1 3 ⇒ x = y 3 − 1 2 ; x = 0 ⇒ y = 1 Thể tích khối tròn xoay được tạo thành khi quay trục Oy hình phẳng gởi hạn bởi đồ thị hàm số y = 2 x + 1 1 3 đường thẳng y=3 và đường thẳng được tính bằng công thức V = π ∫ 1 3 y 3 − 1 2 2 d y = 480 π 7 .

Đáp án D
Phương pháp giải: Công thức tính thể tích của khối tròn xoay là V = π ∫ a b f 2 ( x ) d x
Lời giải: Thể tích khối tròn xoay cần tính là V = π ∫ 1 3 f ( x ) 2 d x
Chọn C.
Tiếp tuyến (d) qua O có dạng y = kx, k > 0. (d) tiếp xúc với (P) tại điểm có hoành độ x 0
khi hệ x 0 2 + m = k x 0 2 x 0 = k > 0 có nghiệm x 0 tức là phương trình x 0 2 = m có nghiệm x 0 > 0 h a y
x 0 = m v à m ≥ 0 suy ra k = 2 m
Phương trình (d): y = 2 m x
Mà V = 6 π suy ra m = ± 6 mà m ≥ 0 suy ra m = 6
Vậy m = 6 thỏa mãn bài toán.