Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân có AB = BC = a. Cạnh bên SA vuông góc với đáy, góc SBA = 60°. Gọi M là điểm nằm trên AC sao cho A C → = 2 C M → . Tính khoảng cách giữaSM và AB.
A. 6 a 7 7
B. a 7 7
C. a 7 21
D. 3 a 7 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
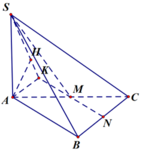
Gọi N là trung điểm của BC.
d A B , S M = d A , S M N
Dưng đường cao AK trong tam giác AMN, dựng đường cao AH trong tam giác SAK.
Dễ dàng chứng minh được A H ⊥ S M N tại H, suy ra d A B , S M = d A , S M N = A H
A K = B N = 2 a , S A = 5 a 3 ⇒ A H = 10 a 3 79

Đáp án B.
Gọi H là hình chiếu vuông góc của S trên (ABC)
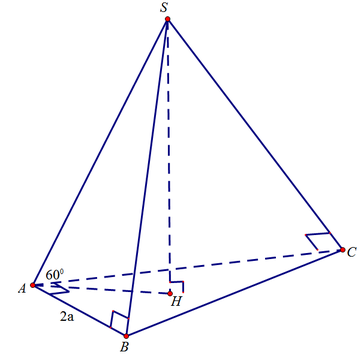
Ta có A C ⊥ S H C ⇒ A C ⊥ H C ⇒ H C / / A B .
Tương tự A B ⊥ S H B ⇒ A B ⊥ H B ⇒ H B / / A C
Vậy H là đỉnh thứ tư của hình vuông BACH như hình vẽ sau:
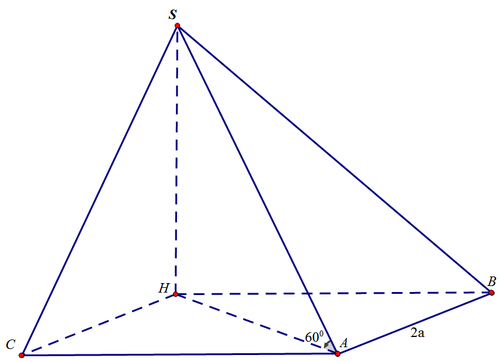
Khi ấy, ta có: A H = 2 a 2 ⇒ S H = 2 a 6
⇒ V S . A B H C = 1 3 S H . S A B H C = 1 3 2 a 6 .4 a 2 = 8 6 a 3 3
⇒ V S . A B C = 1 2 V S . A B H C = 4 6 a 3 3
Chọn D