Cho tam giác ABC nhọn nội tiếp đường tròn (O;R). Hai đường cao BE,CF cắt nhau tại H . AH cắt BC tại D và cắt (O) tại I .
a) Chứng minh H là trực tâm của tam giác ABC và AH BC tại D .
b) Chứng minh AEF ABC và EA.EC EH.EB.
c) Chứng minh 4 điểm A, E, H , F cùng thuộc một đường tròn. Xác định tâm J của đường tròn đó.
d) Kẻ đường kính AK của đường tròn (O;R). Chứng minh BK AB;KC AC từ đó suy ra tứ giác BHCK là hình bình hành

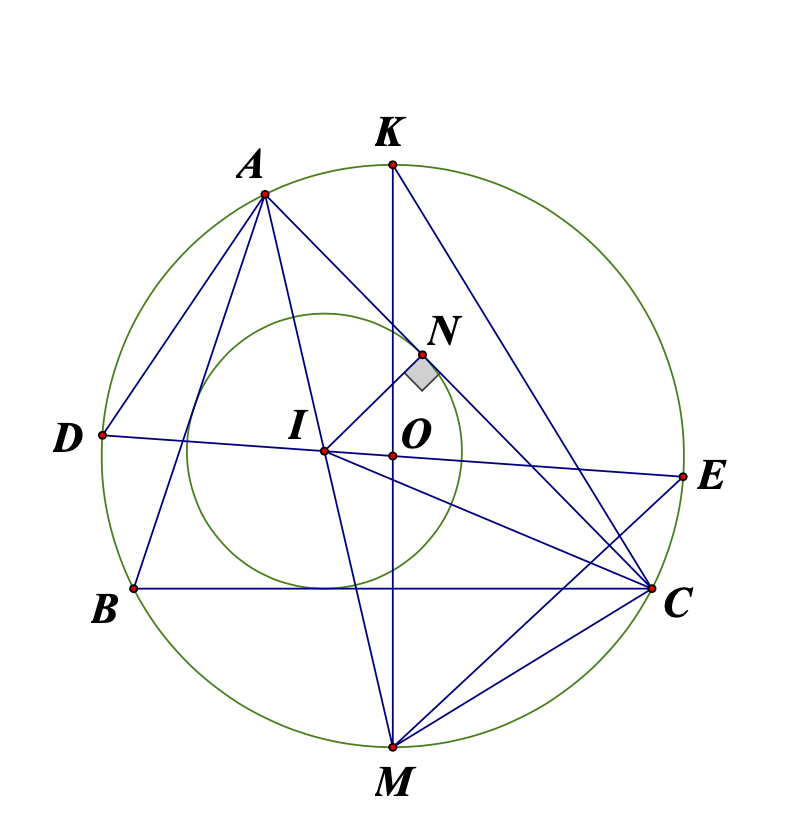
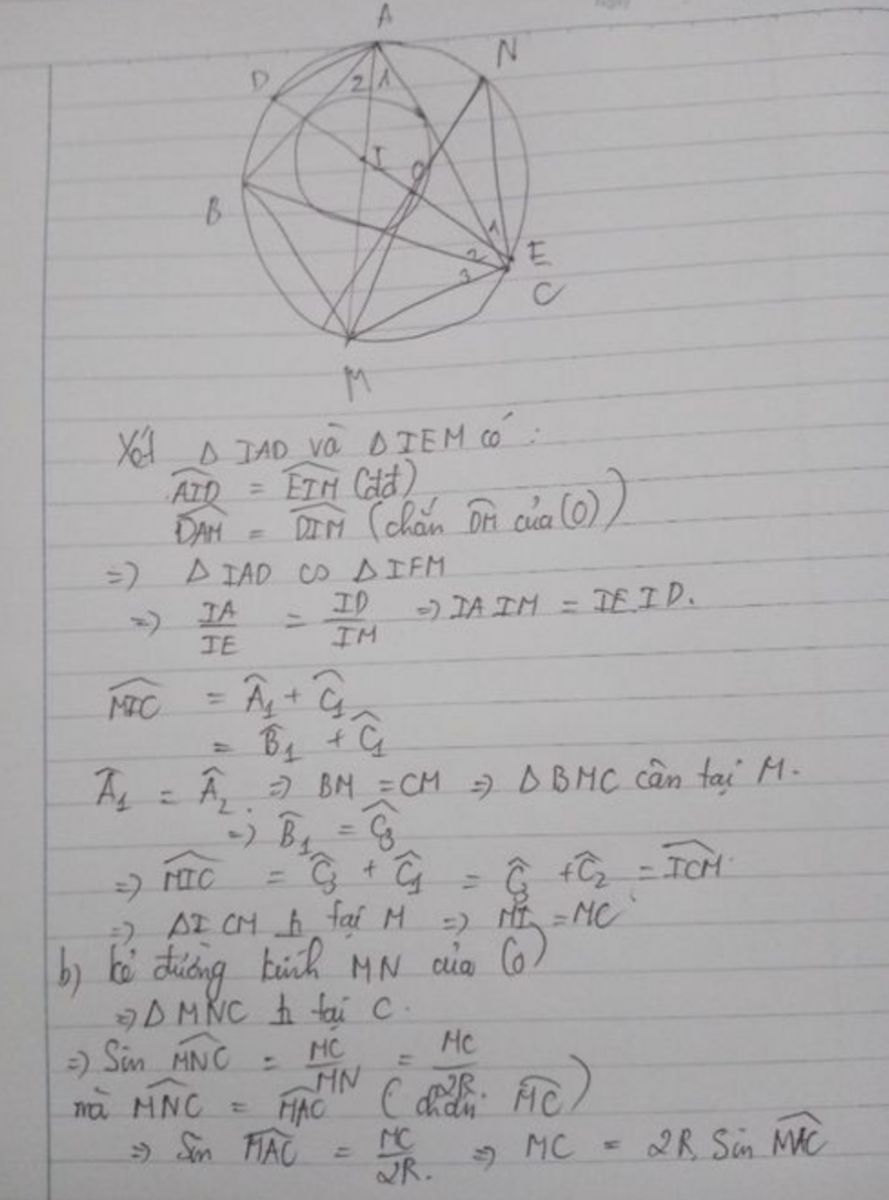
a: Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC