Các bn chỉ mk bs này vs mk cần gấp . Cảm ơn các bn nhiều !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
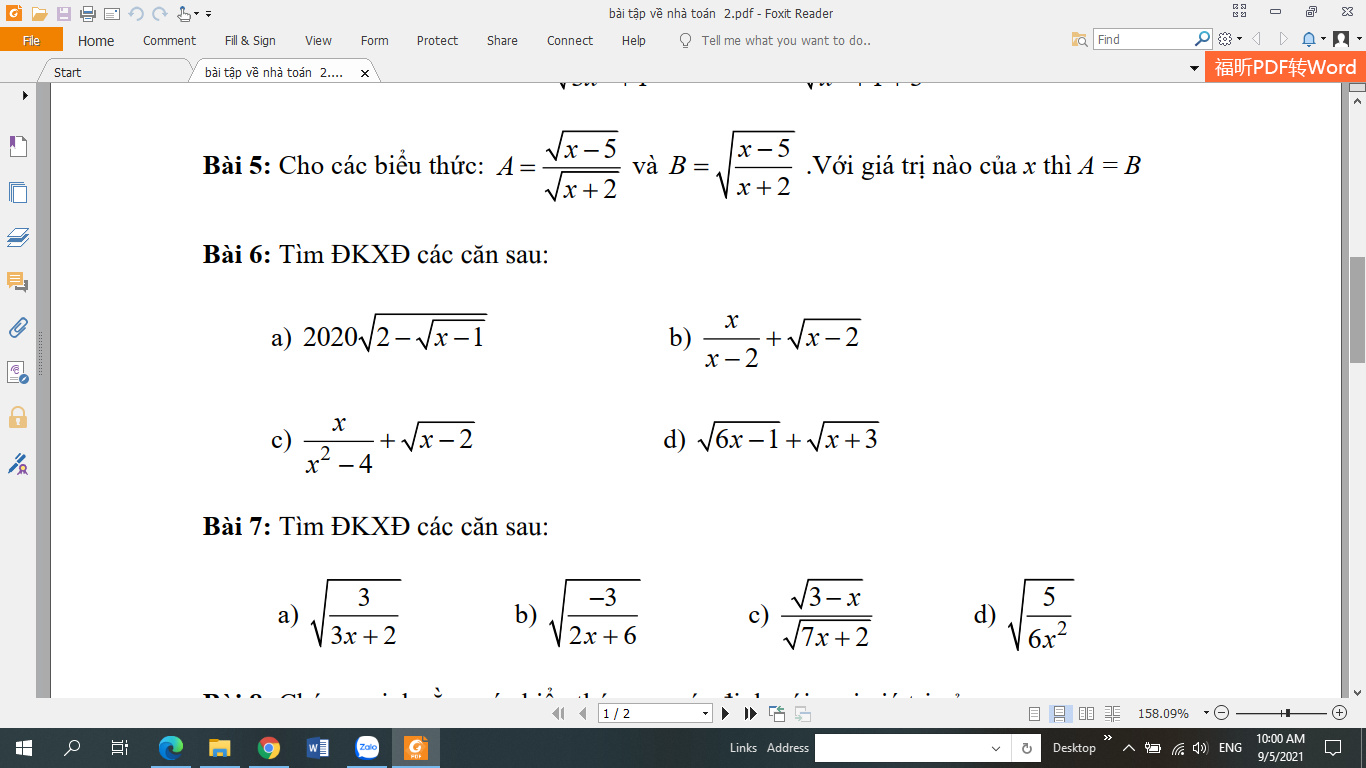
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+2x+3}=a>0\\\sqrt{x^2+x+2}=b>0\end{matrix}\right.\) \(\Rightarrow a^2-b^2=x+1\)
Pt trở thành:
\(a+b=2\left(a^2-b^2\right)\)
\(\Leftrightarrow a+b=\left(2a-2b\right)\left(a+b\right)\)
\(\Leftrightarrow2a-2b=1\) (do \(a+b>0\))
\(\Leftrightarrow2a=2b+1\)
\(\Leftrightarrow2\sqrt{x^2+2x+3}=2\sqrt{x^2+x+2}+1\)
\(\Leftrightarrow4\left(x^2+2x+3\right)=4\left(x^2+x+2\right)+1+4\sqrt{x^2+x+2}\)
\(\Leftrightarrow4x+3=4\sqrt{x^2+x+2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{3}{4}\\16\left(x^2+x+2\right)=\left(4x+3\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{3}{4}\\8x=23\end{matrix}\right.\) \(\Rightarrow x=\dfrac{23}{8}\)
b.
ĐKXĐ: \(x\ge3\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x-3}=a\ge0\\\sqrt{x+2}=b>0\end{matrix}\right.\) \(\Rightarrow a^2-b^2=-5\)
Phương trình trở thành:
\(\left(a-b\right)\left(ab+1\right)=a^2-b^2\)
\(\Leftrightarrow\left(a-b\right)\left(ab+1\right)=\left(a-b\right)\left(a+b\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\left(vô-nghiệm\right)\\ab+1=a+b\end{matrix}\right.\)
\(\Rightarrow ab-a-b+1=0\)
\(\Leftrightarrow\left(a-1\right)\left(b-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x-3}=1\\\sqrt{x+2}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1\left(ktm\right)\end{matrix}\right.\)

2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED

Lời giải:
$x^2\geq 0, \forall x\in\mathbb{R}$
$\Rightarrow Q(x)=x^2+\sqrt{3}\geq \sqrt{3}>0$ với mọi $x\in\mathbb{R}$
Do đó đa thức $Q(x)$ vô nghiệm.

\(\sqrt{\left(2x-5\right)^2}=3\)
\(\Rightarrow\left(2x-5\right)^2=9\)
\(\Rightarrow\left[\begin{array}{nghiempt}2x-5=3\\2x-5=-3\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=4\\x=1\end{array}\right.\)
Vậy x=4 ; x=1
\(\sqrt{\left(2x-5\right)^2}=3\)
\(\Leftrightarrow\left|2x-5\right|=3\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2x-5=3\\2x-5=-3\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=4\\x=1\end{array}\right.\)

a) xy - 5y = 13
y . ( x - 5 ) = 13
Lập bảng ta có :
| x-5 | 13 | 1 | -13 | -1 |
| x | 18 | 6 | -8 | 4 |
| y | 1 | 13 | -1 | -13 |
Vậy ( x ; y ) = ( 18 ; 1 ) = ( 6 ; 13 ) = ( -8 ; -1 ) = ( 4 ; -13 )
# Chúc bạn học tốt ^^!
a) xy - 5y = 13
y . ( x - 5 ) = 13
Lập bảng ta có :
| x-5 | 13 | 1 | -13 | -1 |
| x | 18 | 6 | -8 | 4 |
| y | 1 | 13 | -1 | -13 |
Vậy ( x ; y ) = ( 18 ; 1 ) = ( 6 ; 13 ) = ( -8 ; -1 ) = ( 4 ; -13 )
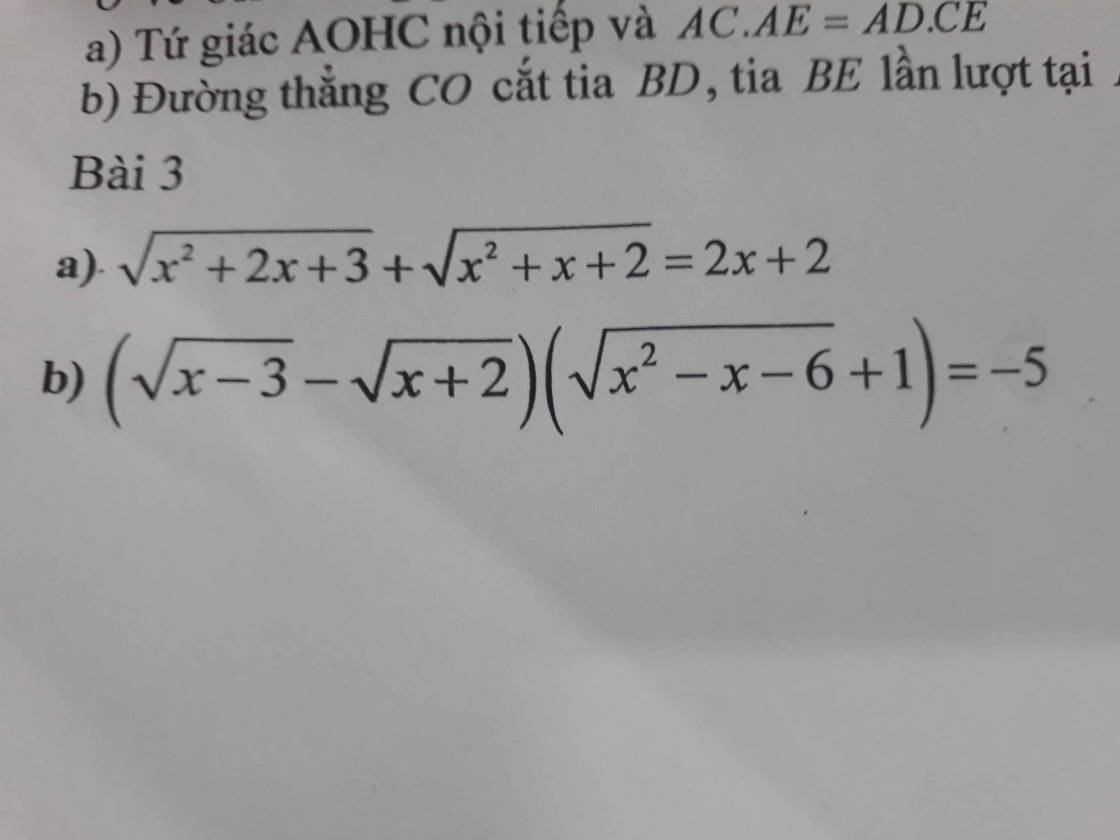

Mik thấy có 5 hình tam giác
Có tất cả là 5 hình tam giác bạn nhé !