Cho hình vẽ sau
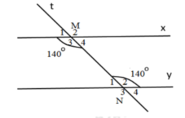
Biết . Tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐE BAI:
Cho hình tam giác ABC . Trên cạnh AB lấy điểm M sao cho AM= 1/3 AB. Trên cạnh AC lấy điển N sao cho AN =1/3 AC.Nối B với N ;nối C với M. Cắt BN và CM cát tai điển I.
A,So sánh S tam giác ABN và S tan giác ACM.
B,So sánh S tan giác BMI cà S tam giác CNI
C,Tính diện tích tam giác ABC ,biết diện tích tứ giác AMIN bằng 90cm2
mình giải thế này có đúng ko
a) tam giác ABN và tam giác ABC chung chiều cao hạ từ B xuống AC ; đáy AN = 1/3 đáy AC
=> S(ABN) = 1/3 xS(ABC)
Tam giác ACM và ACB có chung chiều cao hạ từ C xuống AB ; đáy AM = 1/3 đáy AB
=> S(AMC) = 1/3 x S(ABC)
=> S(AMC) = S(ANB) Vì cùng bằng 1/3 S(ABC)
b) Ta có: S(AMC) = S(CNI) + S(AMIN)
S(ANB) = S(BMI) + S(AMIN)
Mà S(AMC) = S(ANB) nên S(CNI) = S(BMI)
c) Nối A với I:
Ta có: S(AMI) = 1/2 S(BMI) (Vì đáy AM = 1/2 đáy BM ; chung chiều cao hạ từ I xuống AB)
S(ANI) = 1/2 S(CNI)
Mà S(CNI) = S(BMI) nên S(AMI) = S(ANI) = 90 : 2 = 45 cm2
=> S(AIB) = 3 x S(AMI) = 3 x 45 = 135 cm2
=>S(ABN) = S(AIB) + S(AIN) = 135 + 45 = 180 cm2
=> S(ABC) = 3 x S(ABN) = 3 x 180 = 540 cm2

a) Theo đề bài: OM = 3cm, ON = 7cm; \(M,N\in Ox.\)
\(\Rightarrow\) OM < ON.
\(\Rightarrow\) M nằm giữa 2 điểm O và N.
b) Ta có: ON = OM + MN.
Thay: 7 = 3 + MN.
\(\Leftrightarrow\) MN = 7 - 3 = 4 (cm).
a) Theo đề bài: OM = 3cm, ON = 7cm; M,N∈Ox.M,N∈Ox.
⇒⇒ OM < ON.
⇒⇒ M nằm giữa 2 điểm O và N.
b) Ta có: ON = OM + MN.
Thay: 7 = 3 + MN.
⇔ MN = 7 - 3 = 4 (cm).
HT

\(\widehat{MON}=\widehat{xOM}+\widehat{xON}=140^0+40^o=180^o\)
=> M; O; N thẳng hàng
=> MN cắt xx' tạo O => \(\widehat{xON};\widehat{x'OM}\) là hai góc đối đỉnh
![]() Cho đường thẳng xx' và một điểm O nằm trên đường thẳng xx'. Trên nửa mặt phẳng bờ xx', vẽ tia OM sao cho xOM =140% . Trên nửa mặt phẳng bờ xx' không chứa tia OM vẽ tia ON sao cho xON = 40%. chứng minh xON và x' OM là hai góc đối đỉnh.
Cho đường thẳng xx' và một điểm O nằm trên đường thẳng xx'. Trên nửa mặt phẳng bờ xx', vẽ tia OM sao cho xOM =140% . Trên nửa mặt phẳng bờ xx' không chứa tia OM vẽ tia ON sao cho xON = 40%. chứng minh xON và x' OM là hai góc đối đỉnh.![]()
∘

AN=2NC
=>\(S_{ABN}=2\cdot S_{BNC}=200\left(m^2\right)\)
=>\(S_{BMN}=\dfrac{1}{4}\cdot200=50\left(m^2\right)\)
=>\(S_{MNCB}=150\left(m^2\right)\)
bạn có thể giải thích cách làm được không ạ? mình nhìn vẫn chưa hiểu lắm ý...