Cho tam giác ABC có AC > AB, đường cao AD. Trong các khẳng định sau khẳng định nào sai?
A. ∠(ABC) > ∠(ACB)
B. BD < DC
C. Hình chiếu của A lên BC là D
D. ∠(BAD) > ∠(DAC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A là khẳng định sai.
Vì \(SB\perp\left(ABC\right)\) nên \(SB\perp BC\)
Nếu \(SA\perp BC\Rightarrow SA||SB\) hoặc SA trùng SB (đều vô lý)

Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).

Do ∠A là góc tù nên ∠A lớn nhất. Vậy có ∠A> ∠B > ∠C. Từ đó suy ra BC > AC > AB. Chọn (D) BC > AC > AB.

Xét hai tam giác vuông ABC và DFE có: ∠A = ∠D = 90º ; AC=DE
a) Thêm điều kiện BC=EF thì ΔABC=ΔDFE (cạnh huyền - cạnh góc vuông).
b) Thêm điều kiện ∠C = ∠E thì ΔABC=ΔDFE (g.c.g).
c) Thêm điều kiện ∠C = ∠F thì ta không thể kết luận ΔABC=ΔDFE
a) Đúng;
b) Đúng;
c) Sai.

Đáp án D
Ta có: B C ⊥ A A ' B C ⊥ A H
![]()
Do đó:
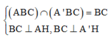
![]()
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
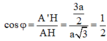
⇒ φ = 60 o
Chọn D