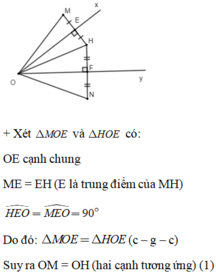
Cho góc nhọn xOy. Lấy điểm H nằm trong góc xOy. Từ H kẻ HE ⊥ Ox tại E, HF ⊥ Oy tại F. Trên tia HE lấy điểm sao cho E là trung điểm của HM, trên tia HF lấy điểm N sao cho F là trung điểm của HN. Khi đó:
A. OM = OH = ON
B. E O F ^ = 1 2 M O N ^
C. Câu A đúng, câu B đúng
D. Câu A đúng, câu B sai