Câu 1: Cho dãy A là dãy giảm gồm N (N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2023
2:
#include <bits/stdc++.h>
using namespace std;
int A[100],ln,nn,vt1,vt2,n;
int main()
{
cin>>n;
for(int i=1; i<=n; i++) cin>>A[i];
ln=A[1];
for (int i=1; i<=n; i++)
ln=max(ln,A[i]);
nn=A[1];
for (int i=1; i<=n; i++)
nn=min(nn,A[i]);
vt1=1; vt2=n;
for (int i=1; i<=n; i++)
if (ln==A[i] && vt1<=i) vt1=i;
for (int i=n; i>=1; i--)
if (nn==A[i] && vt2>=i) vt2=i;
swap(A[vt1],A[vt2]);
for (int i=1; i<=n; i++)
cout<<A[i]<<" ";
}
10 tháng 8 2023
Câu 1: Tính số fibonaci thứ N. biết f(1)= 1; f(2) = 1; f(N)=f(N-2)+F(N-1)
#include <iostream>
int fibonacci(int n) {
if (n <= 2) {
return 1;
}
int prev = 1;
int current = 1;
int fib;
for (int i = 3; i <= n; i++) {
fib = prev + current;
prev = current;
current = fib;
}
return fib;
}
int main() {
int N;
std::cin >> N;
int result = fibonacci(N);
std::cout << "Số Fibonacci thứ " << N << " là: " << result << std::endl;
return 0;
}
10 tháng 8 2023
Câu 2: Cho dãy a gồm m số nguyên (|ai| <=10), dãy b gồm n số nguyên (bị <=10). 2 dãy này đã được sắp xếp không giảm. Hãy in ra một dãy c có các phần tử gồm 2 dãy số trên cũng được sắp xếp không giảm.
#include <iostream>
#include <vector>
std::vector<int> mergeArrays(const std::vector<int>& a, const std::vector<int>& b) {
std::vector<int> c;
int i = 0;
int j = 0;
while (i < a.size() && j < b.size()) {
if (a[i] <= b[j]) {
c.push_back(a[i]);
i++;
} else {
c.push_back(b[j]);
j++;
}
}
while (i < a.size()) {
c.push_back(a[i]);
i++;
}
while (j < b.size()) {
c.push_back(b[j]);
j++;
}
return c;
}
int main() {
int m, n;
std::cin >> m >> n;
std::vector<int> a(m);
std::vector<int> b(n);
for (int i = 0; i < m; i++) {
std::cin >> a[i];
}
for (int i = 0; i < n; i++) {
std::cin >> b[i];
}
std::vector<int> c = mergeArrays(a, b);
std::cout << "Dãy c sau khi sắp xếp không giảm là:" << std::endl;
for (int i = 0; i < c.size(); i++) {
std::cout << c[i] << " ";
}
std::cout << std::endl;
return 0;
}
31 tháng 12 2021
2:
#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
sort(a+1,a+n+1);
for (i=1; i<=n; i++) cout<<a[i]<<" ";
cout<<endl;
for (i=n; i>=1; i--) cout<<a[i]<<" ";
return 0;
}
6 tháng 11
Uses Crt;
Var A : array [1..1000] of longint;
n, m, d, t, i, S, k : longint;
Begin
//Phan A
Clrscr;
Writeln(' Phan A ');
Write(' Ban hay nhap 1 so n bat ky: ');
Readln(n);
Write(' Cac so chia het cho ba tu 1 den ',n,' la: ');
For i:=1 to n do
If (i mod 3) = 0 then Write(' ',i);
//Phan B
Writeln;
Writeln(' Phan B ');
Write(' Ban hay nhap 1 so m bat ky: ');
Readln(m);
For i:=1 to m do
Begin
Write(' Ban hay nhap hang tu thu ',i,': ');
Readln(A[i]);
S:= S+A[i];
End;
Write(' Tong cua day so tren la: ',S);
//Phan C
Writeln;
Writeln(' Phan C ');
Write(' Ban hay nhap 1 so d bat ky: ');
Readln(d);
Write(' Ban hay nhap so K: ');
Readln(k);
For i:=1 to n do
Begin
Write(' Ban hay nhap hang tu thu ',i,': ');
Readln(A[i]);
If ((A[i] div k)=1)then t:=t+1;
End;
Write(' Co tat ca ',t,' so giong ',k);
Readln;
End.
9 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
long long a[200],n,i;
int main()
{
cin>>n;
for (i=1; i<=n; i++)
cin>>a[i];
sort(a+1,a+n+1);
for (i=1; i<=n; i++) cout<<a[i]<<" ";
return 0;
}
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
• Ta có: \({u_{n + 1}} = \frac{{\left( {n + 1} \right) + 1}}{{\left( {n + 1} \right) + 2}} = \frac{{n + 1 + 1}}{{n + 1 + 2}} = \frac{{n + 2}}{{n + 3}}\)
Xét hiệu:
\(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{n + 2}}{{n + 3}} - \frac{{n + 1}}{{n + 2}} = \frac{{{{\left( {n + 2} \right)}^2} - \left( {n + 1} \right)\left( {n + 3} \right)}}{{\left( {n + 3} \right)\left( {n + 2} \right)}} = \frac{{\left( {{n^2} + 4n + 4} \right) - \left( {{n^2} + n + 3n + 3} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{{n^2} + 4n + 4 - {n^2} - n - 3n - 3}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{1}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}\)
Vậy \({u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\). Vậy dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.
• Ta có: \({u_n} = \frac{{n + 1}}{{n + 2}} = \frac{{\left( {n + 2} \right) - 1}}{{n + 2}} = 1 - \frac{1}{{n + 2}}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(n + 2 > 0 \Leftrightarrow \frac{1}{{n + 2}} > 0 \Leftrightarrow 1 - \frac{1}{{n + 2}} < 1 \Leftrightarrow {u_n} < 1\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.
\(n \ge 1 \Leftrightarrow n + 2 \ge 1 + 2 \Leftrightarrow n + 2 \ge 3 \Leftrightarrow \frac{1}{{n + 2}} \le \frac{1}{3} \Leftrightarrow 1 - \frac{1}{{n + 2}} \ge 1 - \frac{1}{3} \Leftrightarrow {u_n} \ge \frac{2}{3}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.
Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.
Chọn A.
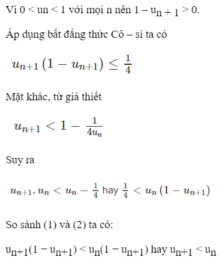
Câu 1: Cho dãy A là dãy giảm gồm N (N<=250) số
nguyên dương A1....AN và số nguyên K. Hãy tìm kiếm số
nguyên K trong dãy A.
A. Xác định bài toán
- B. Viết thuật toán tìm kiếm nhị phân|cho bài
toán. viết 2 cách
#include <bits/stdc++.h>
using namespace std;
long long i,n,x,k;
int main()
{
cin>>n>>k;
for (i=1; i<=n; i++)
{
cin>>x;
if (x==k) cout<<i<<" ";
}
return 0;
}