Cho hai hình cầu A và B lần lượt có bán kính là 3 cm và 6 cm. So sánh diện tích hai mặt cầu của hai hình cầu đó là:
A. S A = S B
B. S A = 2 S B
C. S A = 1 2 S B
D. S A = 1 4 S B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ì 0 < a < b < r ⇒
Vậy đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) có bán kính lớn hơn mặt cầu S(O; r) và mặt phẳng (β)

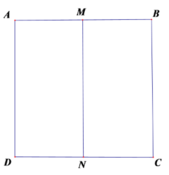
Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có đường cao h = a và bán kính đáy ![]()
Diện tích 1 đáy và diện tích xung quanh của hình trụ là:
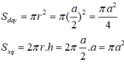
Nên có diện tích toàn phần của hình trụ:
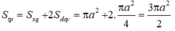
Mặt cầu (S) có bán kính R có diện tích bằng Stp của mặt trụ nên:
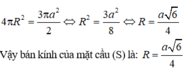

Đáp án C
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.

\(S=4\pi R^2=36\pi\Rightarrow R=3\) \(\Rightarrow OA=3\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH=2\sqrt{2}\)
Pitago tam giác vuông OAH:
\(AH=\sqrt{OA^2-OH^2}=1\)
\(\Rightarrow AB=2AH=2\)

Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
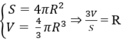
Đáp án là D