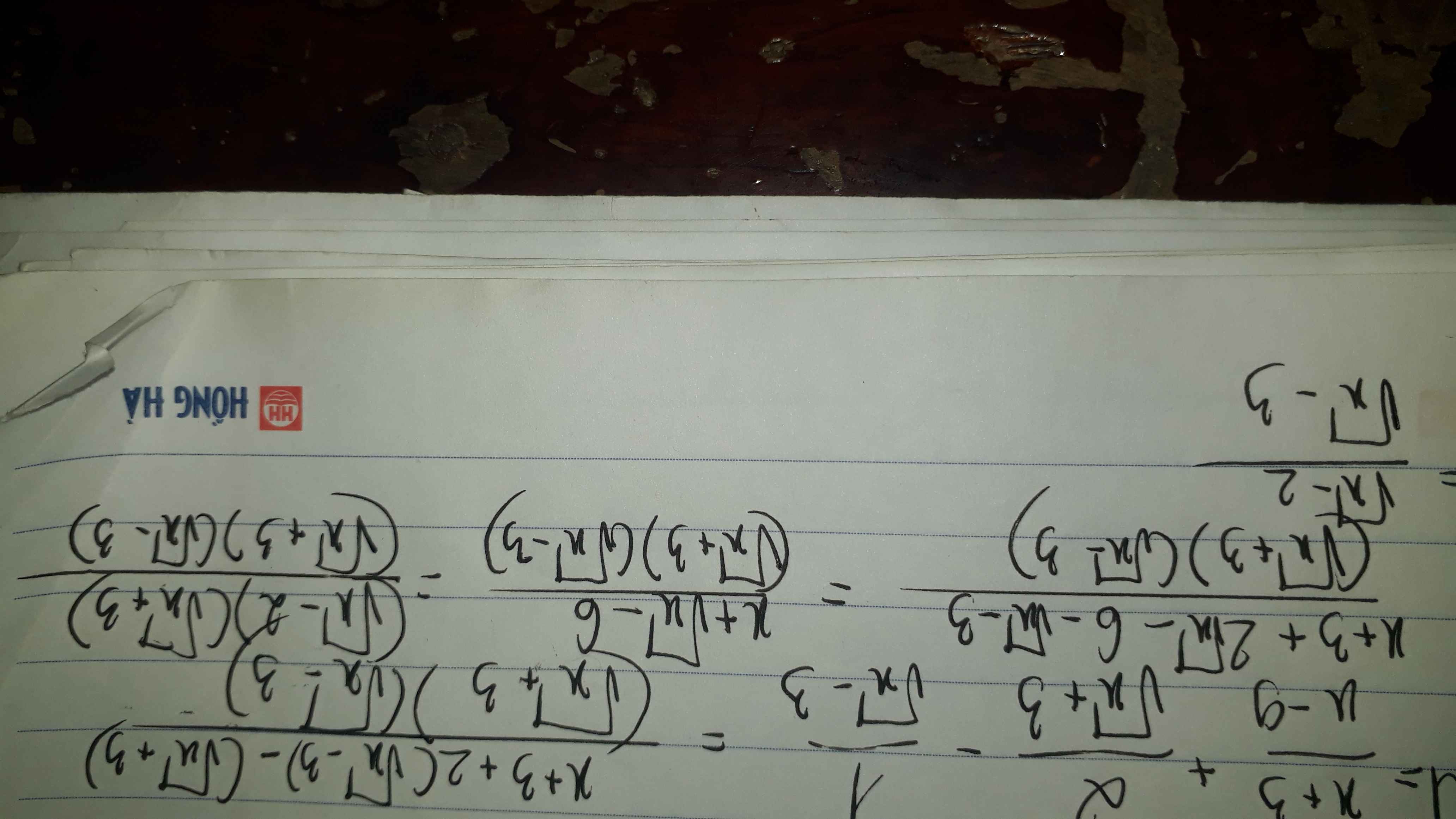Rút gọn biểu thức với ta được?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(M=\left(\dfrac{3}{\sqrt{x}+3}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt{x}-5}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{3.\left(\sqrt{x}-3\right)+x+9}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-5-\left(\sqrt{x}-3\right)}{\sqrt{x}.\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+3\sqrt{x}}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}-2}{\sqrt{x}.\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}.\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}.\left(\sqrt{x}-3\right)}{\sqrt{x}-2}=\dfrac{x}{\sqrt{x}-2}\)
b) \(M< 0\Leftrightarrow\sqrt{x}-2< 0\Leftrightarrow x< 4\)
Kết hợp điều kiện ta được \(0< x< 4\) thì M < 0
c) Từ câu b ta có M < 0 \(\Leftrightarrow0< x< 4\)
nên \(x\inℤ\) để M nguyên âm <=> \(x\in\left\{1;2;3\right\}\)
Thay lần lượt các giá trị vào M được x = 1 thỏa
d) \(M=\dfrac{x}{\sqrt{x}-2}=\sqrt{x}+2+\dfrac{4}{\sqrt{x}-2}=\left(\sqrt{x}-2+\dfrac{4}{\sqrt{x}-2}\right)+4\)
Vì x > 4 nên \(\sqrt{x}-2>0\)
Áp dụng BĐT Cauchy ta có
\(M=\left(\sqrt{x}-2+\dfrac{4}{\sqrt{x}-2}\right)+4\ge2\sqrt{\left(\sqrt{x}-2\right).\dfrac{4}{\sqrt{x}-2}}+4=8\)
Dấu "=" xảy ra khi \(\sqrt{x}-2=\dfrac{4}{\sqrt{x}-2}\Leftrightarrow x=16\left(tm\right)\)
1) \(M=\left(\dfrac{3}{\sqrt[]{x}+3}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5}{x-3\sqrt[]{x}}-\dfrac{1}{\sqrt[]{x}}\right)\left(x>0;x\ne9\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\left(\sqrt[]{x}-3\right)}{\left(\sqrt[]{x}+3\right)\left(\sqrt[]{x}-3\right)}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}-\dfrac{1}{\sqrt[]{x}}\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\sqrt[]{x}-9+x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5-\left(\sqrt[]{x}-3\right)}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\sqrt[]{x}+x}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5-\sqrt[]{x}+3}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{\sqrt[]{x}\left(\sqrt[]{x}+3\right)}{x-9}\right):\left(\dfrac{\sqrt[]{x}-2}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{\sqrt[]{x}}{\sqrt[]{x}-3}\right):\left(\dfrac{\sqrt[]{x}-2}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\dfrac{\sqrt[]{x}}{\sqrt[]{x}-3}.\dfrac{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}{\sqrt[]{x}-2}\)
\(\Leftrightarrow M=\dfrac{x}{\sqrt[]{x}-2}\)
2) Để \(M< 0\) khi và chỉ chi
\(M=\dfrac{x}{\sqrt[]{x}-2}< 0\left(1\right)\)
Nghiệm của tử là \(x=0\)
Nghiệm của mẫu \(\sqrt[]{x}-2=0\Leftrightarrow\sqrt[]{x}=2\Leftrightarrow x=4\)
Lập bảng xét dấu... ta được
\(\left(1\right)\Leftrightarrow0< x< 4\)

a) C = c + d + 2 ( c − d ) 3 = ( 3 c − d ) 3 .
b) D = m − n ( n + p ) 3 = ( m − 2 n − p ) 3 .

\(M=\dfrac{x+3+2\left(\sqrt{x}-3\right)-\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{x+3+2\sqrt{x}-6-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{x+\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\)

Câu 2:
2) Ta có: \(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-\sqrt{x}}{\sqrt{x}-3}\)
Câu 2 :
Gọi : vận tốc của người đi chậm là : x (km/h) ( x > 0 )
Vận tốc của người đi nhanh : x + 4 (km/h)
Vi : người đi chậm đến muộn hơn : 45 phút \(=\dfrac{3}{4}\left(h\right)\)
Khi đó :
\(\dfrac{36}{x}-\dfrac{36}{x+4}=\dfrac{3}{4}\)
\(\Leftrightarrow\left[36\cdot\left(x+4\right)-36x\right]\cdot4=3x\cdot\left(x+4\right)\)
\(\Leftrightarrow3x^2+12x-144=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\left(n\right)\\x=16\left(l\right)\end{matrix}\right.\)

Bài 2:
3x + 2(5 - x) = 0
<=> 3x + 10 - 2x = 0
<=> x + 10 = 0
<=> x = 0 - 10
<=> x = -10
=> x = -10
Bài 3:
6(3q + 4q) - 8(5p - q) + (p - q)
= 6.3p + 6.4q - 8.5p - (-8).q + p - q
= 18p + 24q - 40p + 8q + p - q
= (18p - 40p + p) + (24q + 8q - q)
= -21p + 31q

a) MTC = (x -2)(x + 2). Ta rút gọn được M = 1 x − 2
b) Gợi ý: x 2 + 5 x + 6 = ( x + 2 ) ( x + 3 ) ; x 2 + x − 12 = ( x − 3 ) ( x + 4 )
Ta có N = ( x + 2 ) ( x + 3 ) ( x − 3 ) ( x + 4 ) : ( x + 2 ) 2 x ( x − 3 ) = x ( x + 3 ) ( x + 2 ) ( x + 4 )