Tất cả các giá trị của m để hàm số nghịch biến trên R là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(y'=\frac{2}{3}x+m\geq 0, \forall x\in\mathbb{R}\Leftrightarrow m\geq -\frac{2}{3}x, \forall x\in\mathbb{R}\)
\(\Leftrightarrow m\geq \max (\frac{-2}{3}x), \forall x\in\mathbb{R}\)
Vì $\frac{-2}{3}x$ không có max với mọi $x\in\mathbb{R}$ nên không tồn tại $m$

Chọn D
![]()
![]()
Hàm số có 2 điểm cực trị x 1 , x 2
![]()
Chia y cho y’ ta được :
![]()
Điểm cực trị tương ứng :
![]()
![]()
Với x 1 + x 2 = 4 x 1 x 2 = m + 2 nên y 1 y 2 = ( m - 2 ) 2 ( 4 m + 17 )
Hai cực trị cùng dấu ⇔ y 1 y 2 > 0
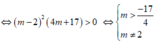
Kết hợp đk : - 17 4 < m < 2

\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)

Hai đường thẳng trên là song song khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2+2m-2=1\\5\ne2m+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\\m\ne1\end{matrix}\right.\)
\(\Leftrightarrow m=-3\)

Đáp án B
Ta có: y ' = 3 m − 1 x 2 − 6 m − 1 x + 3 2 m − 5 .
Để hàm số nghịch biến trên R thì: y ' ≤ 0 ∀ x ∈ ℝ
⇔ 3 m − 1 x 2 − 6 m − 1 x + 3 2 m − 5 ≤ 0 ∀ x ∈ ℝ
⇔ m − 1 x 2 − 2 m − 1 x + 2 m − 5 ≤ 0 ∀ x ∈ ℝ
TH1: m − 1 = 0 ⇔ m = 1 ⇒ − 3 < 0 (luôn đúng)
TH2: m − 1 < 0 Δ ' = m − 1 2 − 2 m − 5 m − 1 ≤ 0 ⇔ m < 1
Vậy m ≤ − 1.