Cho hàm số y = f x xác định, liên tục trên - 1 ; 5 2 và có đồ thị là đường cong như hình vẽ.
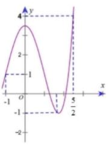
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x trên - 1 ; 5 2 là:
A. M = 4 , m = 1
B. M = 4 , m = - 1
C. M = 7 2 , m = - 1
D. M = 7 2 , m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Từ bảng biến thiên của hàm số y=f(x), suy ra bảng biến thiên của hàm số y = f ( x ) là
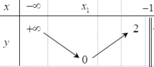

Dựa vào bảng biến thiên, ta suy ra hàm số có 4 điểm cực trị.

Chọn D
Trong khoảng ![]() đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)

Chọn A.
Ta có: y’ = f’(x) + 2cosxsinx = f’(x) + sin2x
y’(x) = 1 ⇔ f’(x) + sin2x = 1 ⇔ f’(x) = 1 – sin2x ⇒ f(x) = x + ½ cos2x.

Đáp án A
Ta có
y ' = f ' x + 2 sin x . cos x = f ' x + sin 2 x
y ' = 1 ⇔ f ' x + sin 2 x = 1 ⇔ f ' x = 1 − sin 2 x ⇒ f x = x + 1 2 cos 2 x
Chọn B.
Dựa vào đồ thị M = 4, m = -1.