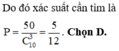Cho đa giác lồi 10 cạnh. Có bao nhiêu tam giác được tạo thành từ các đỉnh của đa giác đã cho?
A. A 10 3
B. 3 10
C. C 10 3
D. 3 10 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Cứ nối 3 điểm bất kì của đa giác tạo thành 1 tam giác nên số tam giác là C 10 3

Đáp án D
Cứ nối 3 điểm bất kì của đa giác tạo thành 1 tam giác nên số tam giác là ![]() .
.

Gọi đa giác là \(A_1A_2...A_{10}\)
a.
Tam giác có 2 cạnh là cạnh đa giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề của đa giác.
Đa giác có 10 bộ 3 đỉnh liền kề (\(A_1A_2A_3;A_2A_3A_4...;A_{10}A_1A_2\)) nên có 10 tam giác thỏa mãn.
b.
Chọn 2 đỉnh liền kề của đa giác: có 10 cách \(\left(A_1A_2;A_2A_3;...;A_{10}A_1\right)\)
Chọn đỉnh còn lại ko liền kề với 2 đỉnh nói trên: có \(10-4=6\) đỉnh (bỏ đi 2 đỉnh đã chọn ban đầu và 2 đỉnh kề với nó)
\(\Rightarrow10.6=60\) tam giác thỏa mãn
c.
Số tam giác bất kì có đỉnh là đỉnh của đa giác: \(C_{10}^3=120\)
Số tam giác ko có cạnh nào là cạnh đa giác: \(120-\left(10+60\right)=50\)

HD: Chọn ra 3 đỉnh bất kỳ của đa giác có: C 10 3 cách chọn.
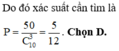
■ Số tam giác có 2 cạnh là cạnh của đa giác là: 10
(vì ứng với mỗi đỉnh ta lấy 2 cạnh kề với nó là được tgiác như điều kiện đã xét)
■ Số tam giác có 1 cạnh là cạnh của đa giác là: 10.6 = 60 vì chọn 1 cạnh của đa giác, ta chọn được 6 đỉnh để tạo tam giác (trừ đi 2 đỉnh của cạnh đó và 2 đỉnh nằm kề sát cạnh đó), mà có 10 cạnh như thế nên có 10.6 = 60
Suy ra số tgiác được tạo thành từ các đường chéo của đa giác là: 120 - 10 - 60 = 50 tam giác.