Question

[Pham Trong Bach]

Cho hàm số f x =   x 2 x       k h i    x < 1, x ≠ 0 0         k h i    x = 0 x     k h i   x ≥ 1 .  Khẳng định nào đúng:

A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn 0 ; 1 .  

B. Hàm số liên tục tại mọi điểm trừ điểm x=0

C. Hàm số liên tục tại mọi điểm điểm thuộc R

D. Hàm số liên tục tại mọi điểm trừ điểm x=1

Answer 1

[Cao Minh Tâm]

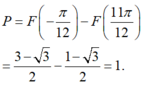
Đáp án C

TXĐ: D=R

  lim x → 0 x 2 x = lim x → 0 x= 0 = f 0

Vậy hàm số liên tục tại x=0

Hàm số liên tục khi x<1

Hàm số liên tục khi x>1

Tại x=1 ta có:

f(1)=1

lim x → 1 − x 2 x = lim x → 1 − x= 1 = f 1

lim x → 1 + x = 1 = f 1

lim x → 1 − f x = lim x → 1 + f x =f 1

Vậy hàm số liên tục tại x=1

Hàm số liên tục trên R